比と前項(後項)の値から後項(前項)の値を求めることができる。 評価規準 比の性質や図を用いて比の一方の値を求める方法を考え、説明している。(数学的な考え方) 問題 ケーキを作るのに、砂糖と小麦粉の重さの比が5:7になるように混ぜます。 練習問題をダウンロード *画像をクリックするとpdfファイルをダウンロード出来ます。 比の文章題1 1124 no22 の別解の途中式にミスがありましたので修正しました。 比の文章題2 比の文章題3 全体を分けて考える問題になります。高校数学の基本問題 Gogle site →数ⅠA →数ⅡB →数Ⅲ (旧C) ***最近の更新*** 反復試行の確率(入試問題) 絶対値付き関数の定積分 Rの関数hist () Rの関数sample () 名義尺度データの比率の検定 フィッシャーの正確

高中数学最容易拿分的题 等差等比数列综合问题 你可千万别丢分 知乎
比 問題 解き方
比 問題 解き方-面積比を使った問題(基礎編) 面積比を使った問題(中級編) 面積比を使った問題(応用編) まとめ! 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! こちらの関連記事はいかがでしょうか?ここで用いた「隣辺比」について、次の問題で見ておきます。 c問題1 右図の三角形abcの面積は斜線部分の面積の何倍ですか。 基本の考え方区切り面積 前出の「区切り面積(高さが等しい三角形の面積比)」を利用しますが、




高中数学最容易拿分的题 等差等比数列综合问题 你可千万别丢分 知乎
比の計算をしよう 比を使った計算練習問題です.等号で結ばれた同じ比で,虫食い部分がある問題.問いの比を簡単な整数で表す問題を用意しています. 数値の大きさは,他のドリルと同様に調整できます. 例1:比の虫食い部分を埋めましょう 618= 6定番問題というよりは、 2辺の比から面積の比を求める基本問題の逆算パターンです。 「隣辺比」 と呼ばれる解き方です。 右の図のように、 三角形abcと三角形adeで「ひとつの角(角a)が共通(重なっている)」とき、 面積の比はその共通角をはさむ2辺の<練習問題> ある草野球チームの去年1年間の試合結果の勝ち負けの比は、5:4であった。 今年は11試合勝ったところ、去年からの通算して勝ち負けの比は7:5になった。 今年と去年の試合数は同じであり、また、この間引き分けはなかった。
黄金比は様々な場面で登場します,まずは最も重要な性質を紹介します。 性質1 黄金比は方程式 x 2 − x − 1 = 0 x^2x1=0 x2 −x− 1 = 0 の解である。 性質1は二次方程式を実際に解くことで簡単に確認できます。 黄金比の定義と見ることもできます。 数学 小6算数「比」の問題 どこよりも簡単な解き方・求め方 kazunokazu 21年6月29日 / 21年7月22日 『今日の算数の授業むずかしかったな3:1に100掛けたのが300:100と比として表します 同じ数を掛けても比は等しいですね! 比と比の値 算数問題プリント集 比の問題 基本 比の問題① 比の問題② 比の問題③
症状② "比の扱い"が不慣れ 面積比の問題の多くは、「比の合成」というテクニックや、図形の面積を分数で表現する解き方などが要求されます。 そのため、"比の扱い"が不慣れのままではなかなか答えにたどり着けません。 症状③ 図の中から"型 比と比の値を習うと次に出てくるのが文章問題です。一見難しそうに見えますがやり方を分かれば簡単ですので一緒に頑張りましょう! それでは早速問題です。 比の一方の数量を求める まさとさんのクラスの男子と女子の人数の比は56で、男子は15人です。問題番号がボタンになっています。 3人の金額の比は,300 : 250 : 150 = 6 : 5 : 3 となります。 このように,3つ以上の項がある場合の比を,連比(れんぴ)といいます。



比の計算ドリル




博客來 你會問問題嗎 問對問題比回答問題 更重要 從正確發問 找出答案到形成策略 百位成功企業家教你如何精準提問 帶出學習型高成長團隊 十五週年暢銷經典 最新增訂版
「疫学と保健統計」試験問題集 以下の問題で適切な答を指示に従って1つまたは2つ選ぶか、解答を数値で記入しなさい。 回答は解答用紙に記入すること。 (1)疫学の説明で不適切な説明はどれか。 1 流行病に関する学門 2 リスク評価のための統計学 3中学3年生 数学 面積の比と体積の比 練習問題プリント 無料ダウンロード・印刷 基本的な立体の相似の意味と、相似な図形の相似比と面積比、および体積比の関係について理解し、問題で練習します。比の応用問題 こちらは、比の応用問題を載せているページです。 比の詳しい解説はこちら 、 基本問題はこちら 、 標準問題はこちら へどうぞ。 (応用問題1) 分数が出てきましたが、連比の考え方を使って求めていきます。 まずは「A全体の面積




关于轴压比的问题思考 上海同瑞土木工程技术有限公司




美国国会史上首次比白宫更支持巴勒斯坦 美国 半岛电视台
比の基本問題の一覧 <比x比,比÷比,比の1あたりの量> 右の表は5年生と6年生が・・・・ <比の1あたりの量> 兄は1050円,弟は750円持っていました。 2人で同じ金額を出し合ってボールを1個買ったところ,残りの金額の比は3:1になりました。 ボールは 算数「平面図形と比(1)」中学受験 中学受験 受験算数でも頻出の「平面図形と比」を取り上げます。 図形問題は、図形や数値など、問題から得られる「見えている情報」から、いかに「見えていない情報」を引き出すかがカギ。 それには、図形に比の表し方を考えさせ、比の値(あたい)の意味を教えます。 問題 めんつゆ量とおゆの量の比が10:50の時、 めんつゆ量は、おゆの量の何倍になっていますか? 式を考えます もとになる数を比べる数でわった商を比の値といいます。




隨筆誌 二上3 1平面向量的運算 面積比問題



初中数学方法与技巧 特殊四边形中的面积比问题 复习
三角比を用いた代表的な計算問題をマスターしましょう。この記事では「様々な三角比の四則演算」「等式を証明するもの」「sin, cos, tan の値を計算するもの」「式の値を計算するもの」についてまとめました。本記事で取り上げた問題はどれも定期試験頻出。 比の応用問題を解く手順 以上の手順をまとめると次の通りです。 1 線分図を描いて比を視覚化する。 2 変化しない線分の比を比べる。 3 比を か にそろえる。 4問題 次の比例式の計算をしましょう。 問1~2は比の値を分数で求めましょう。問3~7はyの値を求めましょう。 比の解き方を覚えて計算力を身につけてください。 問1. 5:7 問2. 1:3=2:6 問3. 1:2=3:y 問4. 2:3=y:6 問5. 3:y=7:15 問6. y:5=1:9




高中数学最容易拿分的题 等差等比数列综合问题 你可千万别丢分 知乎




スマホok 6年 比 比の利用 文章問題 Youtube
割合と比も1の和と差に関する問題と同様で中学入試、高校入試で頻繁に出題される問題です。 和差算を解く上でも"比"を使って解くやり方があったと思います。 この割合や比を苦手とする多くは百分率や歩合、分数を少数にできなかっ 続きを数学35章図形と相似「平行線と線分の比」<準備問題> 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ,条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。・比の基にする量を求めたり、比の値を使ったりして、比の一方の数量を求める問題を解く。 (応用する活動) (説明する活動) ・比の考えを使って、身近な問題を進んで解決しようとしている。 算数への関心・意欲・態度




周長 面積 比 在平面幾何問題中的巧用 每日頭條




比 の計算と文章問題 計算ドリル 問題集 数学fun
平行線と比の利用、辺の長さを求める問題をパターン別解説!←今回の記事 木の高さを求める方法について解説! 中点連結定理を使った問題を解説! 相似の面積比を求める問題をイチからやってみよう! 面積比!平行四辺形の面積問題を解説! 面積比!算数 比の文章題ドリルのページへようこそ 上記のボタンから算数 比の文章題ドリル (PDFプリント・問題集)がダウンロードできます。 個人利用は無料です (家庭以外での配布は有料です)。 プリント内の数字はランダムです。 大量にありますので、お好き練習問題 練習問題+解答 組合せの総数 n C r が整数であることの証明確率 例題(8) 練習問題 練習問題+解答整数の性質 例題(11) 練習問題 練習問題+解答図形の性質 例題(18) 練習問題 練習問題+解答 三角形の角の二等分線と比 メネラウスの定理



Www Boyo Org Tw Boyo Downloads Category 46 17 11 06 01 36 57 Download 32 E5 9c 8b E4 B8 Ad E7 94 9f E4 B8 80 E5 Ae 9a E8 A6 81 E6 9c E7 9a 84 E6 87 E7 94 A8 E9 A1 8c E5 9e 8b E4 B8 E9 A1 8c12 E4 B8 E6 95 B8 E9 87 8f E5 95 8f E9 A1 8c E8 A3 E7 Ad 94 E7




高中数学最容易拿分的题 等差等比数列综合问题 你可千万别丢分 知乎
問題2の答え 1950円 解説 1/11 まず、このような図を書いて解いていきましょう。 補充問題 ( のところにマウスを近づけると、答えが表示されます。はじめ、兄と弟が持っている金額の比は9:5でした。中学受験の算数・理科ヘクトパスカルによる,四谷大塚予習シリーズ算数「速さと比の問題」の手書き解説です。A地からB地までは1 6 km B地からC地までは12kmあります。太郎君は,自転車に乗ってA地を出発し,B地を通ってC地まで一定の速さで走ったところ,出発してから36分後にB地を通過し 比に関する問題です。 小学校で習うレベルの基本的な内容をまずは理解するようにしてください。 →無料で使える学習ドリル 比の問題 中学受験では、複雑な小数や分数の比、単位をそろえて考える問題などはよく出題されます。 確実に




等差数列奇偶项问题 等差数列奇偶公式推导 等比数列前n项和公式




方法总比问题多
目標習得時間:1時間 問題数:4問 この単元では「三角比」という新しい概念が導入されます。新しい概念だけに、覚えなければいけないことも多いのですが、実は公式さえ覚えてしまえばほとんどの問題が解けてしまう、比較的易しい単元です。 数iの「三角比」は、数iiに登場する「三角相似比の練習問題(平行四辺形5) 問1図のように、平行四辺形ABCD の辺AD 上にAE:ED =1:2 となる点E をとり、E から 辺AB に平行な直線を引き、辺BC との交点をF とします。線分比→平行 問題(3 学期) 次の文は,三角形と線分の比についての定理である。( ) をうめよ。 abc で,辺ab,ac 上の点を,それぞれp,q とする。 (1) pq // bc ならば, ap:ab=aq:( ア )=pq:( イ ) (2) ap:pb=aq:qc ならば,pq // ( ウ ) 解答欄 ア イ



比熊犬劈叉姿勢 標準到讓網友懷疑有問題 看獸醫發現別的問題卻笑噴




隨筆誌 一下3 1比例式 汽車速率與機車速率比問題



数学 相似三角形系列03 面积比问题



印度疫情猛船員供給恐出包 專家 問題比塞船更大條 新聞 Moneydj理財網




問題前的 預防 遠比問題後的 處理 來的重要 危機邊界




一年級下冊數學誰比誰多誰比誰少應用題專項練習 每日頭條




等比數列求和等比數列的求和公式 百度文庫 Gkgnae



1




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




博客來 方法總比問題多 打造不找借口找方法的一流員工




等比數列實戰題



6年算数比とその利用2等しい比の教え方




高中数学最容易拿分的题 等差等比数列综合问题 你可千万别丢分 知乎



比熊犬劈叉姿勢 標準到讓網友懷疑有問題 看獸醫發現別的問題卻笑噴




等比數列實戰題




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




隨筆誌 二上3 1平面向量的運算 面積比問題




隨筆誌 一下1 2數列與級數 等差數列特定條件成等比數列相關問題




6年生算数ドリル 比と比の値




一年級下冊數學誰比誰多誰比誰少應用題專項練習 壹讀




高中数学最容易拿分的题 等差等比数列综合问题 你可千万别丢分 知乎




正比與反比大綱 比與比值比的運算性質比例式比例式的運算蘇德宙台灣數位學習科技股份有限公司 Ppt Download




問題數學無窮等比級數 課業板 Meteor 學生社群




Bruno 方法總比問題多 辦法總比困難多 董事長碎碎念



Www Boyo Org Tw Boyo Downloads Category 46 17 11 06 01 36 57 Download 3291 E5 9c 8b E4 B8 Ad E7 94 9f E4 B8 80 E5 Ae 9a E8 A6 81 E6 9c E7 9a 84 E6 87 E7 94 A8 E9 A1 8c E5 9e 8b E4 B8 E9 A1 8c10 E6 95 B8 E5 Ad 97 E5 B0 8d E8 Bf E5 95 8f E9 A1 8c E8 A3 E7 Ad 94 E7




等差数列前n项和之比问题




辦法總比困難多 Itw01




二年級數學應用題大全彙總和差倍數問題附電子版 雪花新闻



Priori Moe Gov Tw Download m 7 Nc 13 5 Pdf




Bruno 方法總比問題多 辦法總比困難多 董事長碎碎念




6年生算数ドリル 比と比の値




算数 練習問題プリント 栄光ゼミナール ちびむすドリル 小学生学習教材 スペシャルコラボ



無窮等比級數的問題 高一數學 紀算補習班 數學補習班 三重 文理補習班 國小數學 國中數學 隨意窩xuite日誌



数学 相似三角形系列03 面积比问题




05 等比数列中的比例问题等比数列高中数学 Youtube




博客來 辦法總比問題多 電子書



印度第二波疫情远比第一波凶险问题出在哪里 Abc News




等比數列實戰題



初中数学方法与技巧 特殊四边形中的面积比问题 复习



ドリルズ 小学6年生 算数 の無料学習プリント比 比率 の問題




博客來 方法總比問題多



名師課輔網 倍比定律的問題




問題數學無窮等比級數和 課業板 Meteor 學生社群



数学 相似三角形系列03 面积比问题




比與比值比例式應用問題自我評量 Ppt Download




6年生算数ドリル 比と比の値




05 等比数列中的比例问题等比数列高中数学 Youtube



1




問題數學無窮等比級數和 課業板 Meteor 學生社群



会议室标语图片会议室布置图片企业会议室标语企业文化墙图片企业文化图片企业会议室标语 只要思想不滑坡 方法总比问题多 企业会议室标语 管理理念挂图标语 企业文化墙 文化墙 企业文化墙 公司文化墙 校园文化墙 工厂标语 医院标语 养生标语 品质标语 会议室标语



房市觀點 我們還能理性地討論公設比問題嗎 股市 Yahoo奇摩行動版




Herman Yeung Blog 學術問題之部分回應 Maths Core A S G S 等差 等比數列 15 Mar 16



数学 相似三角形系列03 面积比问题




奧數 練習 比與比例問題的練習題 每日頭條




等比中項 數列問題中的特殊性質 如果在等比數列a項和b項中 插入一個數g 百科知識中文網




連比例式應用問題比與比例式 Qaxnl
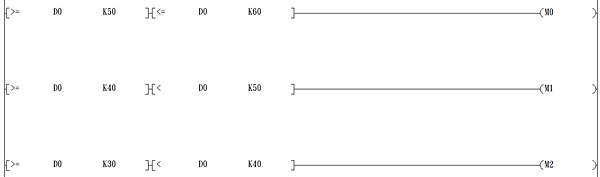



回覆 Yua 的問題 比對d值 觸發指定m接點 Labview Plc還未出師的小工程師部落格 痞客邦




比例式的應用問題 Youtube




均一影片 例題 連比與連比例式1 學習單 Shareclass




方法总比困难多 新人首单立减十元 21年8月 淘宝海外



工信部通报侵害用户权益app 腾讯应用宝问题占比最大 工信部 App 腾讯应用宝 新浪科技 新浪网




比與比值比例式應用問題自我評量 Ppt Download



Q Tbn And9gct1cbhyzmpnguh0uf5t8bdkm4iqdb3jmof2blp0iaelv3tnivk8 Usqp Cau



求教 在ads中设计圆极化天线的轴比问题 微波eda网




小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




應用解題篇第12回連比問題 Youtube




數學本質比 正比與反比陳小婷ppt Download




方法总比问题多




六個關鍵問題 快速了解緬甸政變 紐約時報中文網
.JPG)



小細節大關鍵理解題意趁早開始 翻轉教育




博客來 關鍵課題思考 比解決問題更重要 速效達成目標的超精準工作法




比 解決問題 更核心的關鍵商務能力 Cheers快樂工作人




連比例式應用問題比與比例式 Qaxnl




干货 高中数学 概率 几个易错点 不掌握会拖你后腿 知乎



比熊犬注射疫苗中的4个常见问题 狗狗常见病 波奇网百科大全
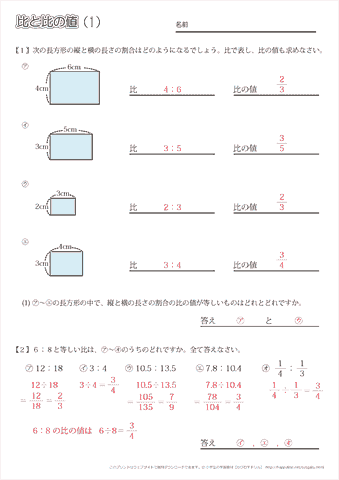



小学6年生の算数 比と比の利用 練習問題プリント ちびむすドリル 小学生




高中数学最容易拿分的题 等差等比数列综合问题 你可千万别丢分 知乎




小學數學比和比例問題知識匯總及解析例題 每日頭條




埃及首次會面蘇丹商討衣索比亞大壩問題 國際焦點 全球 聯合新聞網




隨筆誌 二上3 1平面向量的運算 面積比問題




奧數 練習 比與比例問題的練習題 每日頭條




一年級下冊數學誰比誰多誰比誰少應用題專項練習 壹讀



高中數學 等比數列中的符號問題 稍不注意就會功虧一簣 雪花新闻




G 自由能的問題 考試板 Dcard




小學數學正反比例問題 應用比和比例的性質 參考倍比問題去解決 每日頭條




隨筆誌 一上3 5指數與對數的應用 半衰期等比級數問題



1




等比數列實戰題




Klzm4jbfbnfbim




五年级数学详案单元比17



0 件のコメント:
コメントを投稿