垂心の性質《証明》 三角形の垂心がもつ性質の証明をします。 まずは「 四角形adhf,behd,cfheは円に内接する四角形である 」を証明していきます。 これには、中学3年生で習った 円周角の定理 を使うと理解が早いです。いて証明しようとしている。 ④ 平行線と線分の比につい ての性質を,平行線の性質 や三角形の相似条件を用い て証明することができる。 ⑤ 平行線と線分の比につい ての性質を,記号を用いて 表したり,その意味を読み 取ったりすることができる。16 相似比と面積の比の関係,およびその利用 2 17 立体の相似 18 相似な立体について,相似比と表面積の比,体積の 比の関係 4 相 似 の 利 用 1 19 相似な図形の性質を活用して,影の長さから校舎の 高さを求める方法を考える。

2 の解答の であるから と書いてあるんですが Clear
比の性質 証明
比の性質 証明-3 比例式が条件の等式の証明を扱った問題を解いてみよう 31 問(1)の解答・解説;一般に、整数 N の m 乗根 (ただし、 m は 1 より大きい整数、 N は m 乗数でない整数) 対数のうち、 log 2 3, 並びに log 2 5;



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Syosu Html
式を余弦定理・正弦定理を用いて証明する。そ してこの証明で用いだ性質について検討する。 2 三角比の定義についての検討 2 l標準的な三角比の定義 三角比の定義での角aは,はじめ直角三角形 について考えるため,鋭角,つぎに鈍角へと進 む。一般に、 log m n (ただし、 m, n は 1 より大きい整数で、 m = N a, n = N b を満たす整数 N, a, b が存 二等分線の性質の逆 角の二等分線の長さ 三角形の内角・外角の二等分線の性質は,中学数学で習う基本的で重要な性質です.それらの主張とその証明を紹介します.さらに,後半では発展的内容として,角の二等分線の長さについても紹介します. ⇨
合同な図形の基本性質とは? 三角形の合同条件を使って、合同な三角形を見つける方法! 証明の書き方合同な三角形の証明問題の書き方を基礎から解説! 直角三角形証明問題の書き方とは?合同条件の使い方を徹底解説! ① 比例式の「比」とは、簡単に言うと「割合」のことを指す。 ②比例式とは、 a b = c d のような、「 2 つの比の値が等しい」ということを示した式 ③比例式は「外項の積=内項の積」という性質をもつ ④比例式は2つの数だけでなく3つ以上の数についても表すことができ、これを連比と性質1:隣接する二項は互いに素 フィボナッチ数列: 1,1,2,3,5,8,13,21,34,55 について, どの隣り合う2項も,互いに素(最大公約数は1)です。 例えば, 21 21 21 と 34 34 34 の最大公約数は1です。 これを証明してみましょう。
比例式とは下のような2つの比が等しいですよ、 ab = cd ということを表した等式のことですね。 どういうときに2つの比が等しいっていえるかというと、比の値が等しいときなんです。 比が ab のとき 比の値は a/b になります。平行線と線分の比という内容について解説してきます。 ここでは、相似な図形の性質をつかって いろんな図形の辺の長さを求めていきます。 長々と解説をするよりも 問題を見ながら、実践を通して学習するのが良いので 三角形と平行線の線分の比 まずは 三角形と平行線の線分の比の ルールを覚えましょう。 ポイントは ①2つの辺が平行であれば ②どの辺の比の関係が成り立つのか を押さえる というところになります。




平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
比をみるとイはアの3倍になっている。 T このように比の値が同じ時2つの比は等しいといって次のようにかきます。 40:50 = 1:150 比の値と比の性質,2つの考え方を整理し,等しい比の意味をおさえる。 3 等しい比の性質を理解する。 T2/5時 ・ 平行線と線分の比に関する性質を理解する。 ・ 平行線と線分の比の性質を利用して、辺の長さを求めることができる。 前時のまとめを基に、平行線と線分の比の性質について確認する。 本時の学習内容「平行線と線分の比の関係について第二次 平行線と線分の比の性質を,平行線の性質 ・証明の方針としてまとめるために,整 や三角形の相似条件を用いて証明する。(7) 理したことの間のつながりを考える。 ・証明としての形式的な表現等



1




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ
比の性質 次の相似比を学ぶために比の性質について学んでおこう。 を 比の値 といいました。 これは二年生式の計算の 「比について」 で説明したよね。 この比の値が等しい時二つの比は等しいということができます。 比の値が等しいから、 2 つの比ウ 平行線と線分の比についての性質を見いだし,それらを確かめること。 エ 基本的な立体の相似の意味と,相似な図形の相似比と面積比及び体積比の関係について理解す ること。 の性質を証明するここんにちは、ウチダです。 今日は、中学3年生で習う 「平行線と線分の比の定理」 を用いる問題や、その $3$ 通りの証明、また定理の逆の証明について、わかりやすく解説していきます。 平行線と線分の比の定理とは台形 まずは定理のご紹介です。
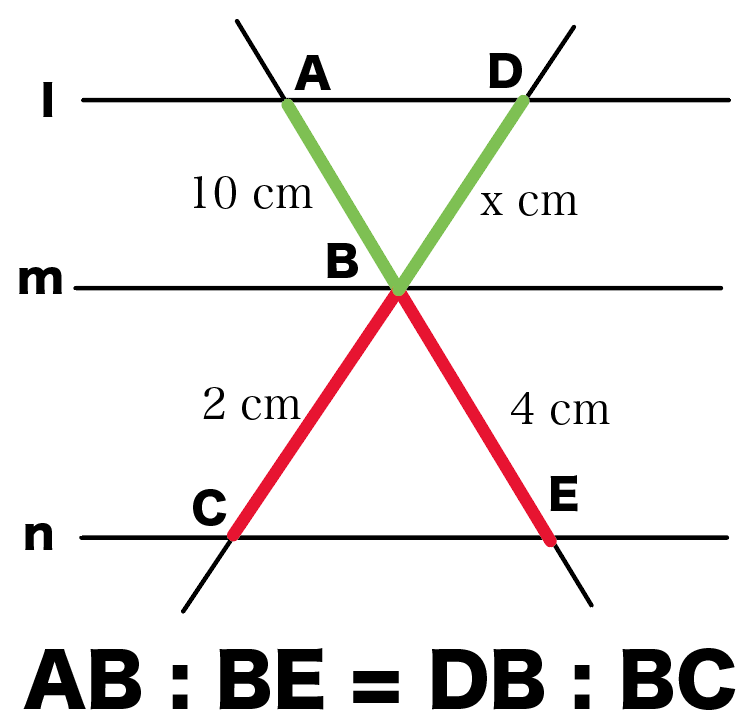



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
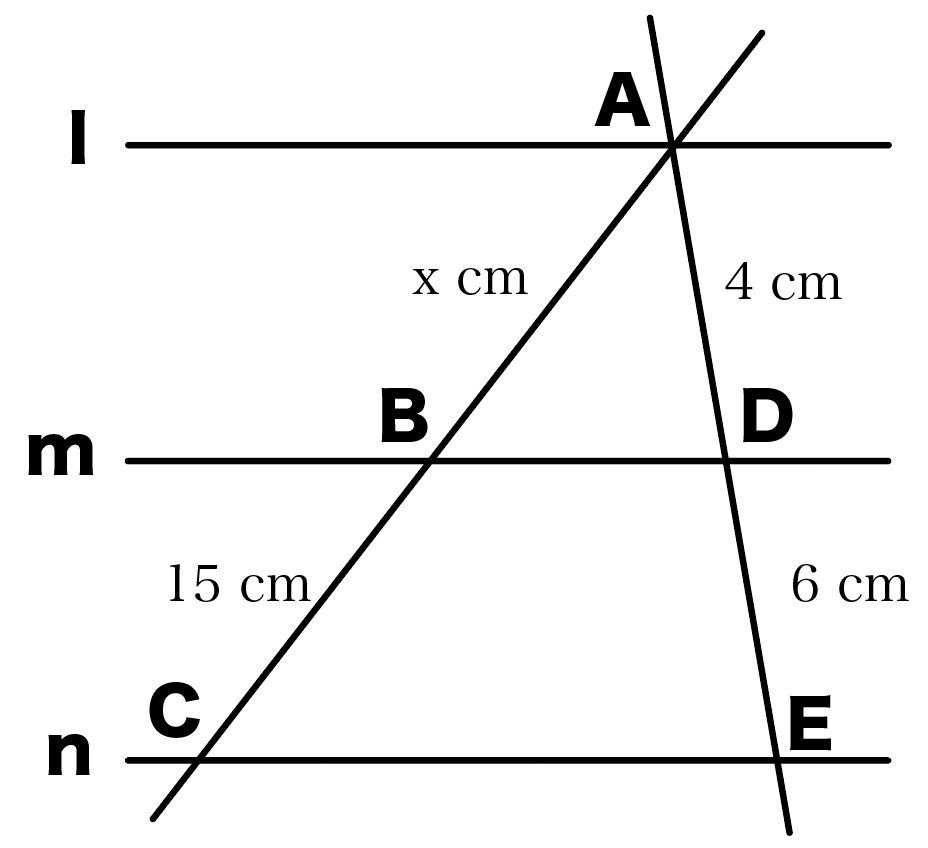



平行線と線分の比の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
1 最小二乗法① 数学的性質 経済統計分析 (13年度秋学期) (参考資料) 2 回帰分析と最小二乗法 被説明変数y tの動きを説明変数x tの動きで説明=回帰分析 説明変数が1つ ⇒ 単回帰 説明変数が2つ以上 ⇒ 重回帰 説明できない部分が小さくなるように回帰式の係数(証明) CからADに平行な直線を引き、Abとの交点をEとする。 よって、 ACEは二等辺三角形、AE=AC。 ADとECが平行より、AB:AE=BD:DC、 AE=ACだから、AB:AC=BD:DC。 性質③、④をまとめると、\(4\) つの三角形の面積比は次のようになります。 台形の性質は丸暗記する必要はありませんが、 どうして性質が成り立つのかを理解しておく と、問題を解いているときに「そういえば」と思い出しやすくなりますよ!




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



Ws Higo Ed Jp Kumaws Cabinets Cabinet Files Download 16 Fedbe972b965c7cadf04 Frame Id 31
になるね。だから比例式の性質、 が成り立つんだね。 そして、 比例式の性質はあたかも「比の外側同士」「比の内側同士」の項をかけてるようにみえるよね?? だから、ちまたでは「比例式の性質」のことを、 外項の積・内項の積 って呼ぶことがあるん第1章 土の基本的性質 粒子の組合せ 土塊内部の粒子の幾何学的配置・粒子 の性質 → 外部からは見えないが土 塊の性質を決定している 連続体としての土塊の性質 → 工学・技術の対象 粒子の性質 (粒度分布) ・異なる大きさの粒子の混じり具合三角形の五心の覚えておくべき性質を整理 レベル ★ 最難関大受験対策 平面図形 更新日時 三角形の五心の定義と重要な性質をまとめました。 三角形の五心は有名で豊かな性質を持っており,数学オリンピックの初等幾何の証明問題では超頻出




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




角の2等分線によって分ける比 身勝手な主張
次に,\ bad}に角{b}の二等分線と辺の比の関係}を適用する このとき,\ {BC=7とBDDC=56を元にBDの長さを求める必要がある} {基準点をOとする位置ベクトルで表現すると式が対称的で美しくなる・ 平行線と線分の比の性質を使って証明を考えることができる。 ・ 平行線と線分の比の性質を利用して、辺の長さを求めることができる。今までに証明した事実を用いて、上記の比の関係を証明しました。 まずは、中点連結定理です。 中学校での、中点連結定理の取り扱いって、昔は合同を用いて「証明する内容」 だったのですけども、最近は 「公理的に扱われる三角形の相似条件」の特殊な



48s96ub7b0z5f Net Sankakukansuu Seishitsu




三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
比と前項(後項)の値から後項(前項)の値を求めることができる。 評価規準 比の性質や図を用いて比の一方の値を求める方法を考え、説明している。(数学的な考え方) 問題 ケーキを作るのに、砂糖と小麦粉の重さの比が5:7になるように混ぜます。 基本3等号で繋げた比の内側の数字の積と外側の数字の積は等しい 「 2:3=4:6 2 : 3 = 4 : 6 」のように等号で繋がれた比の内側と外側の積に着目しましょう。 内側の積: 3× 4=12 3 × 4 = 12 外側の積: 2× 6=12 2 × 6 = 12指導案データベースの新着 指導案データベースについて 学習指導案(ひな形) 検索 キーワード一覧 全19件 (1~10件) 分類 単元・題材名 単元・題材ダウンロードファイル




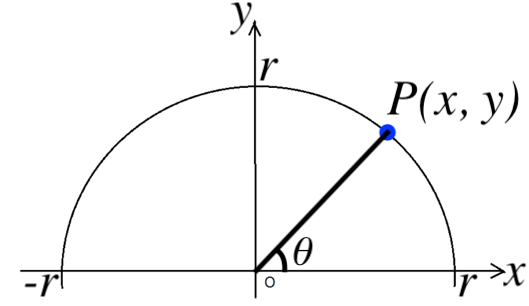
高校数学 単位円を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 0 180 の三角比 受験の月




年度用 中学校数学教科書内容解説資料 未来へひろがる数学
=== 平行線と線分の比 === 三角形の相似条件 次の(1)(2)(3)は三角形の相似条件と呼ばれており,そのうち1つでも成り立てば2つの三角形は相似になる. 逆に,2つの三角形が相似であるとき,次の(1)(2)(3)はすべて成り立つ.なお,線分を黄金比で分けることを,黄金分割 (Golden Section)という. 7.おわりに 今回は,黄金比の定義や基本的な性質について言 及したが,フィボナッチ数列との関係等,黄金比に は,他にも面白い性質が沢山ある.また,黄金比は無理数の例 以下の実数は無理数である。 2の平方根 、または3の平方根;



比の性質について A B C Dがad になるのは何故ですか Yahoo 知恵袋
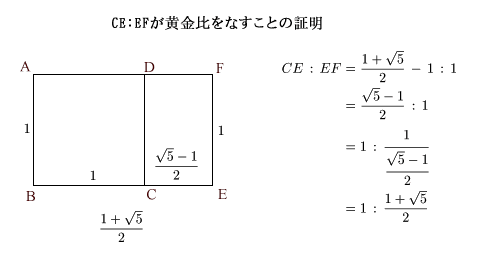



黄金比
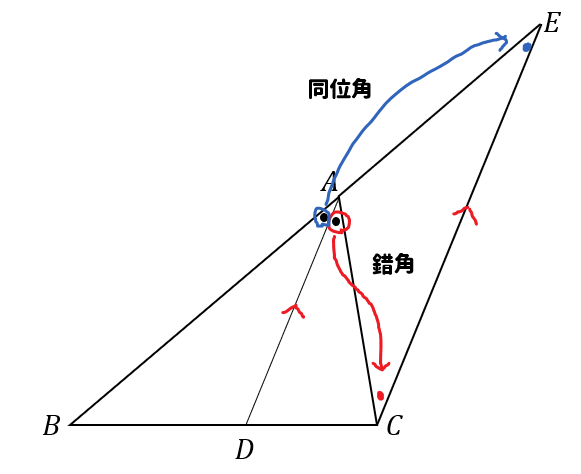



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
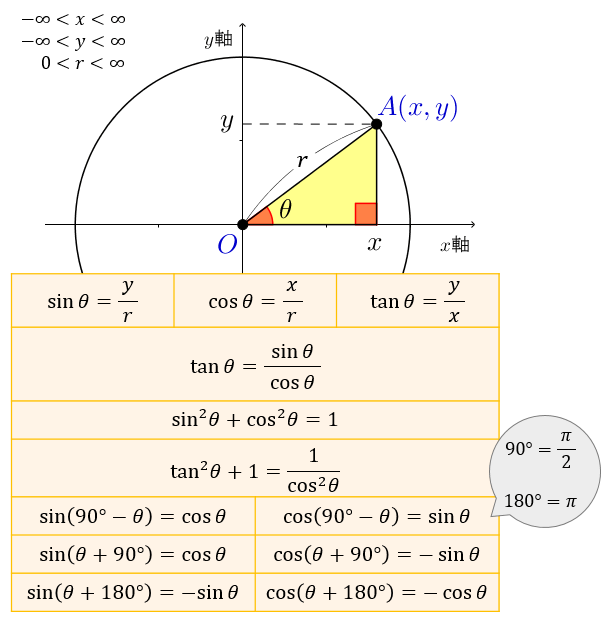



三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典



Www Kyoto Be Ne Jp Ed Center Tangensp 8syudata Chu3su Zukeisouji Tangen Pdf



1




算数 小学生 中学受験 算数 比と比の性質 前半 Youtube
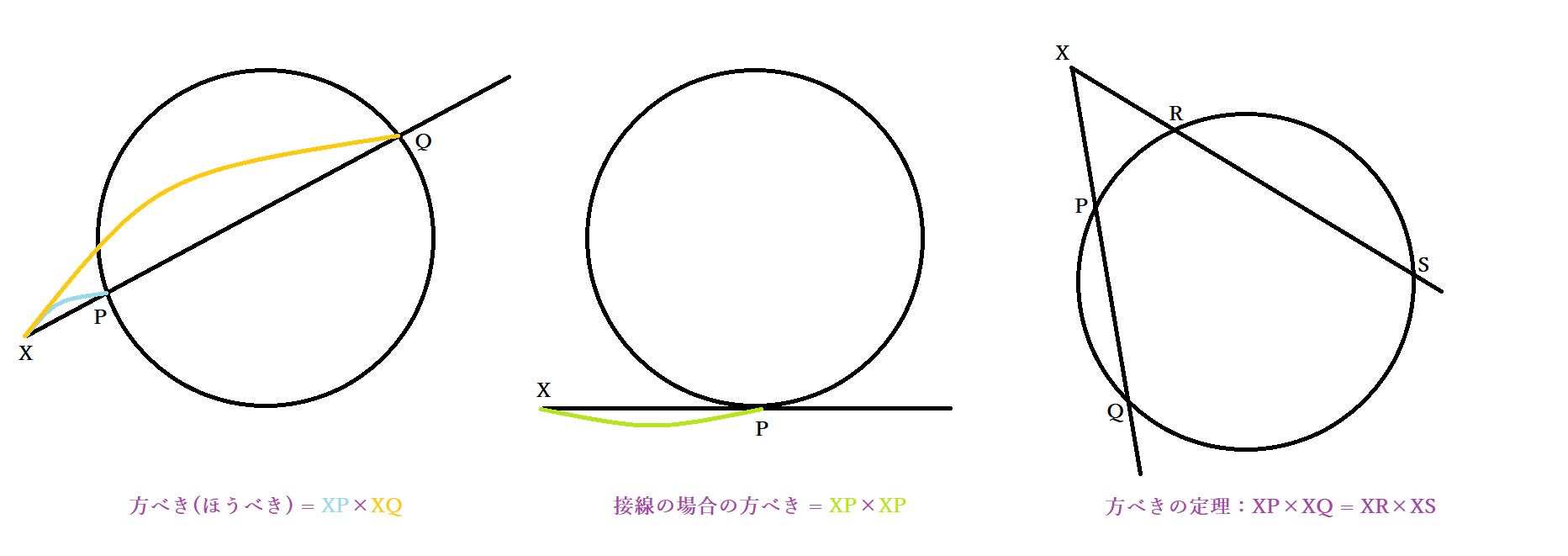



ほうべきの定理とは 方べきの定理の公式を角度や比で証明 中学での問題も Curlpingの幸せblog




三角比完全網羅 三角比 Sinとcosとtanの定義 覚え方 性質 定理 公式 合格サプリ




比と比の値 身勝手な主張
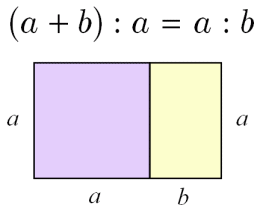



数列 黄金比 を計算する方法 大人が学び直す数学
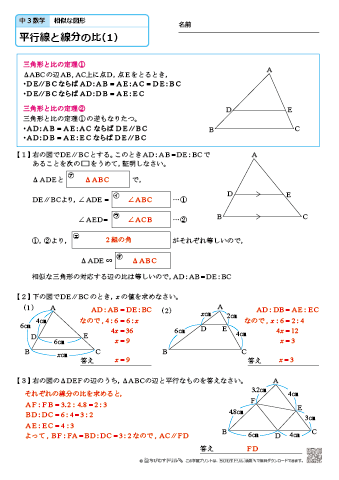



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学ia 三角比とは何か 定義を明らかにしつつ三角比の問題を解く Himokuri




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




3 4 5の三角形で 本当に直角ができる Note Board



1



角の二等分線とは 定理や比の性質 証明 問題 作図方法 受験辞典
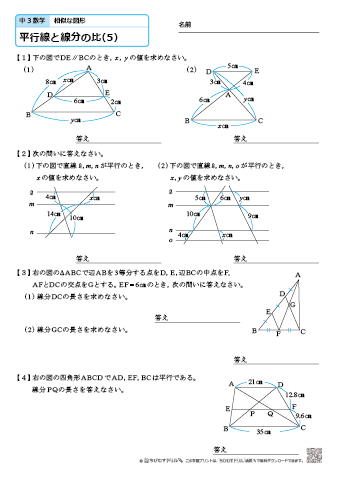



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




複比の定義と複比が不変であることの証明 高校数学の美しい物語




比の値って結局なんなの 苦手な数学を簡単に



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月




数探高校講座 数学 図形と計量 22 三角比の性質 2 数学探究所




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




余弦定理
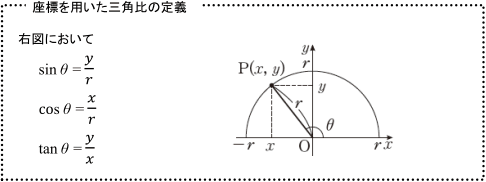



90 以上の角の三角比の値について 数学 苦手解決q A 進研ゼミ高校講座




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
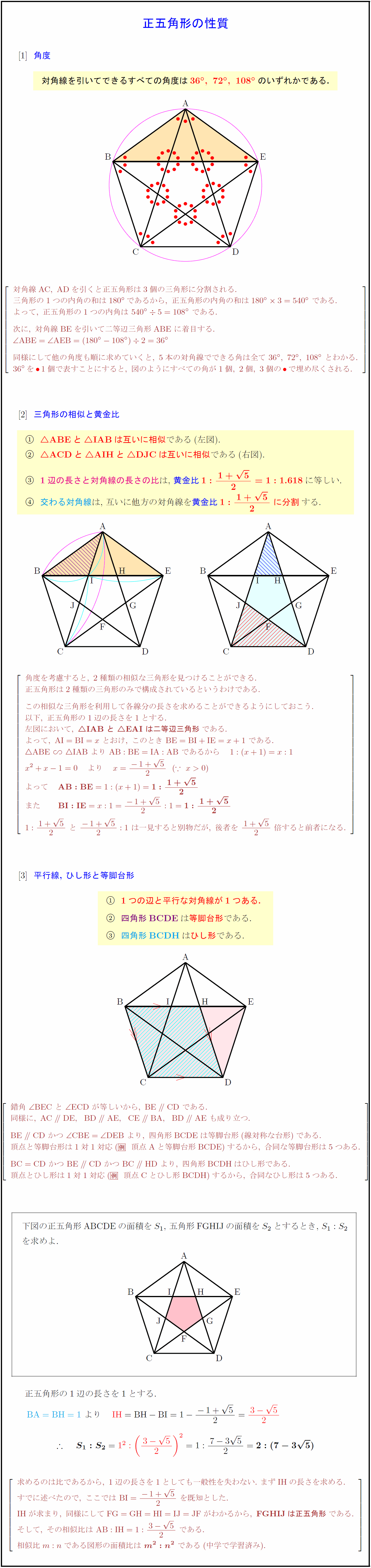



高校数学a 正五角形の性質 三角形の相似 黄金比 等脚台形 ひし形 受験の月




数学1a青チャートの問題です 黄色の蛍光ペンで引いているところですが Ag G M Clear




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月
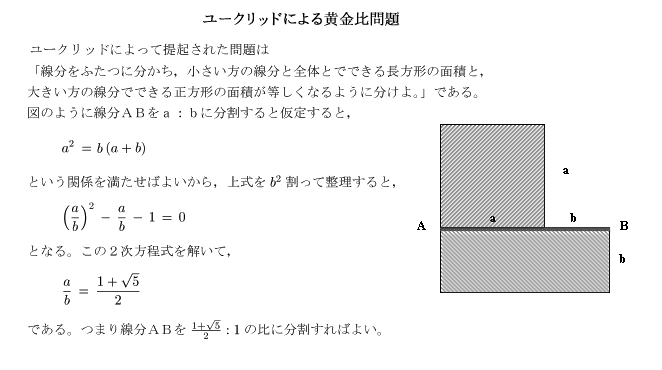



黄金比




平行線と線分比の性質を用いるのは分かっています Clear




基本 三角比の相互関係 なかけんの数学ノート




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




数学 中3 49 平行線と線分の比 基本編 Youtube
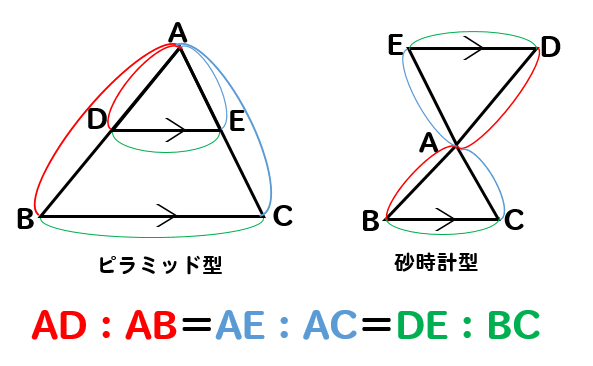



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
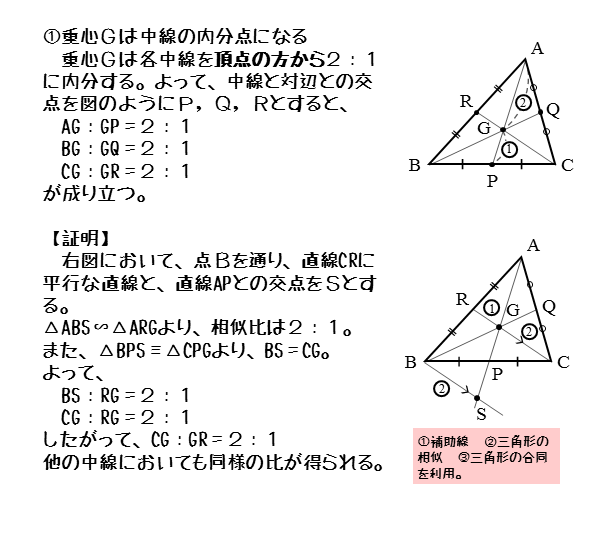



図形の性質 重心について 日々是鍛錬 ひびこれたんれん
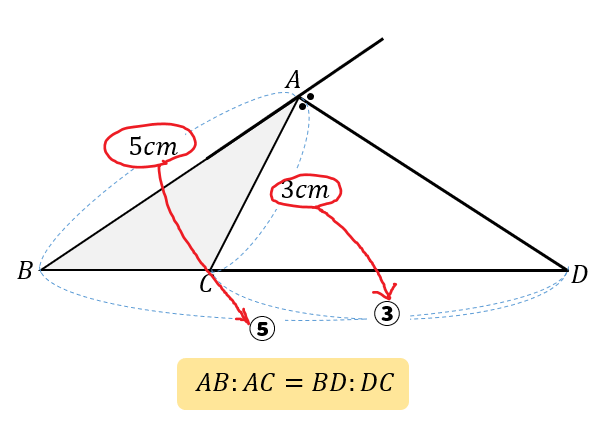



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




もう一つの白銀比 黄金比の一般化 数学 統計教室の和から株式会社



数学外角の二等分線の性質について 外角の二等分線がなぜあのような比に Yahoo 知恵袋




黄金比




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学
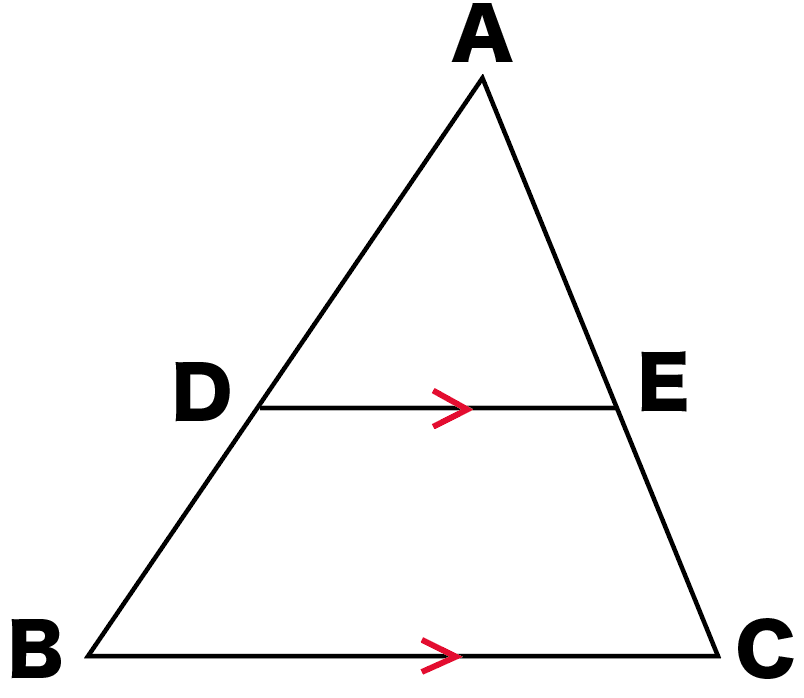



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく
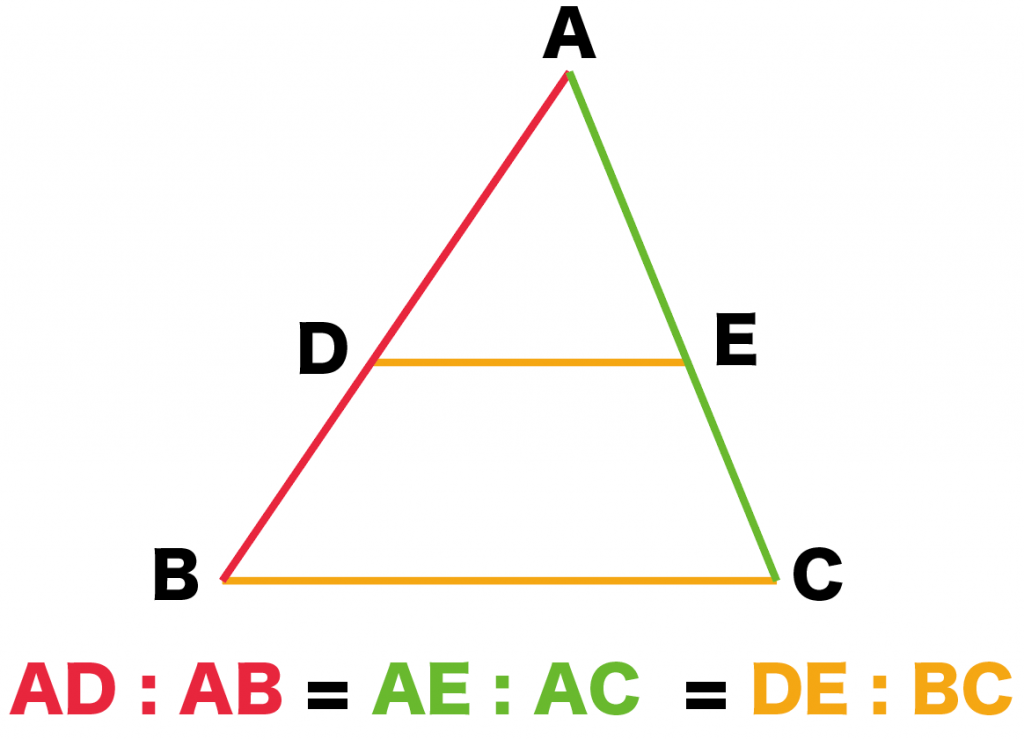



3分でわかる 平行線と線分の比の2つの証明 Qikeru 学びを楽しくわかりやすく




比の性質 Youtube



高等学校数学 授業実践事例のページ




数探高校講座 数学 図形と計量 22 三角比の性質 2 数学探究所




サクッと解説 角の二等分線と比の特徴となぜ について 数スタ




平行線と線分の比の問題 3通りの証明 定理の逆の証明を解説 遊ぶ数学




基本 三角比の定義 直角三角形による定義 なかけんの数学ノート




内角の二等分線 外角の二等分線の比の定理 証明 Youtube




2 の解答の であるから と書いてあるんですが Clear




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Syosu Html



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
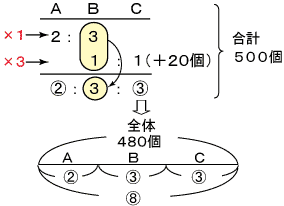



第8章 比の性質 の 偏差値アップ 指導法 例題 中学受験の勉強法 偏差値アップの学習法



Fdk3a7ctb5192box5b Com Es 6nen Mt Hi Seishitsu Syosu Html



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor



1



比の性質について A B C Dがad になるのは何故ですか Yahoo 知恵袋




平行線と線分の比 中学校数学 2018年度高崎経済大学経済学部 地域政策学部入試問題 身勝手な主張
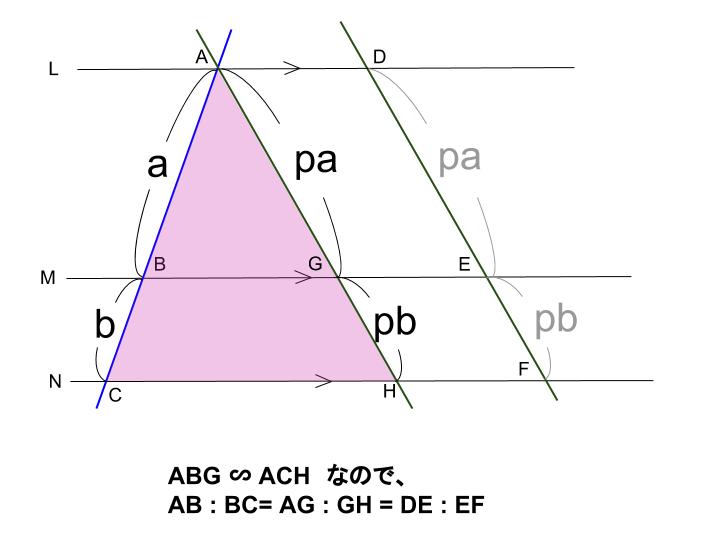



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su
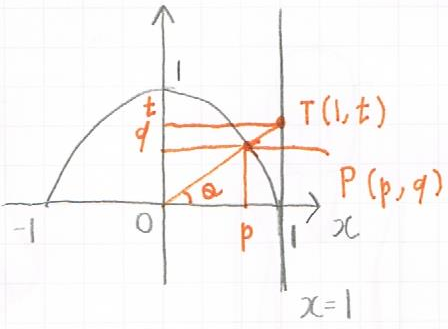



三角比の性質のまとめとその証明




角の二等分線の性質 線分比の公式 に関する定理の証明 理系ラボ
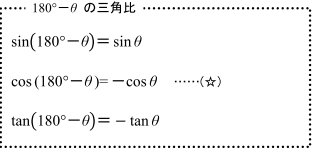



180 8の三角比 数学 苦手解決q A 進研ゼミ高校講座



三角比の公式をしっかり理解しよう スタディクラブ情報局
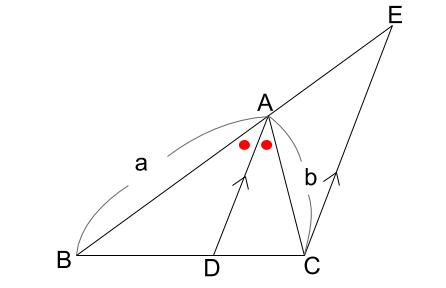



角の2等分と線分の比 中学数学の無料オンライン学習サイトchu Su



三角比 三角関数を総まとめ 定義や各種公式 重要記事一覧 受験辞典




数学ia 三角比とは何か 定義を明らかにしつつ三角比の問題を解く Himokuri




比の性質 Youtube




説明できる 比例式 内項の積 外項の積 小学生にも理解しやすい President Online プレジデントオンライン




角の二等分線と辺の比 の証明 問題の解き方 数学fun




平行線と比の性質の利用 Clear




等比数列の公式まとめ 一般項 和の公式 証明 理系ラボ




高校数学b 等比数列をなす3数の3通りの表現 等比中項 受験の月




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月
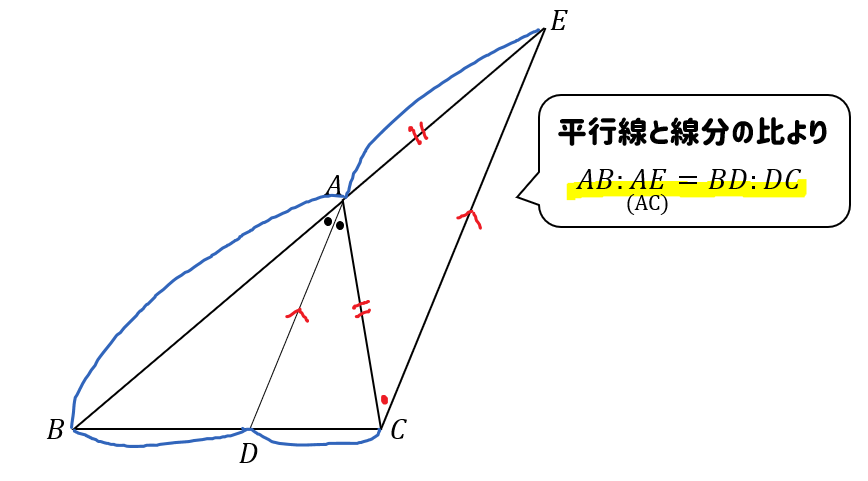



サクッと解説 角の二等分線と比の特徴となぜ について 数スタ



角の二等分線の性質と二等分線の長さ 思考力を鍛える数学
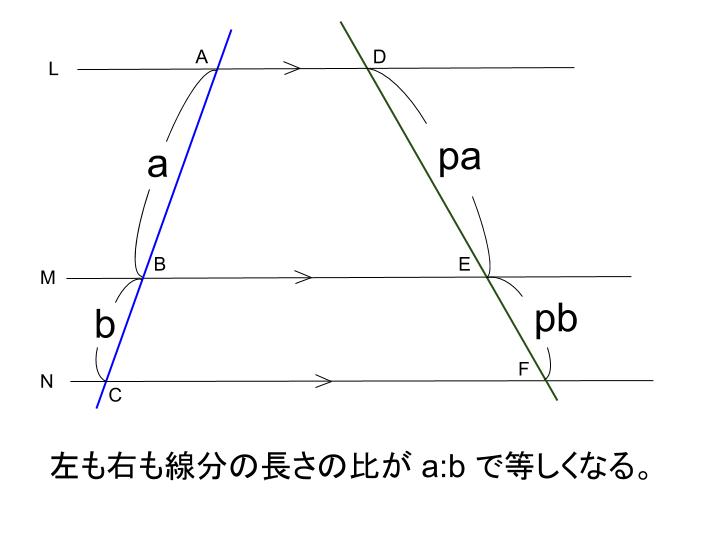



中学数学 平行線と線分の比 その1 中学数学の無料オンライン学習サイトchu Su




三角比の公式をしっかり理解しよう スタディクラブ情報局




数学ia 三角比とは何か 定義を明らかにしつつ三角比の問題を解く Himokuri




数学ia 三角比とは何か 定義を明らかにしつつ三角比の問題を解く Himokuri




図形 の記事一覧 受験辞典



0 件のコメント:
コメントを投稿