200以上 おうぎ形の面積の公式 306214-扇形の面積の公式

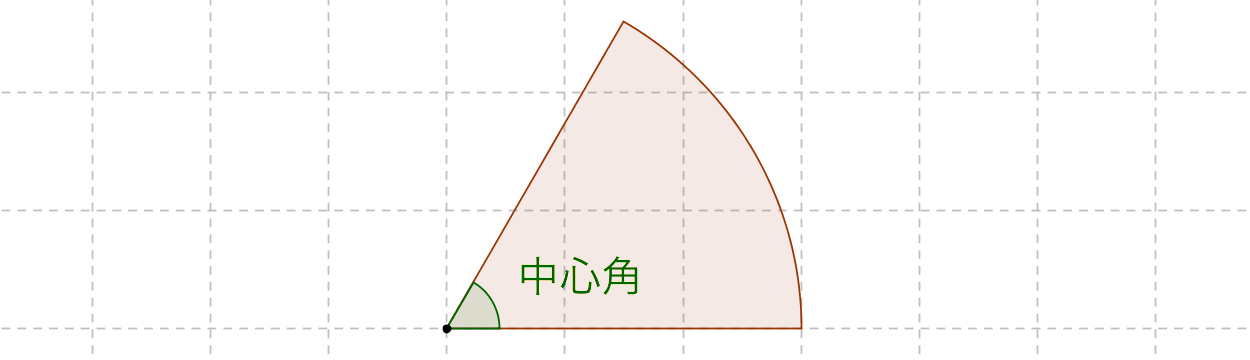
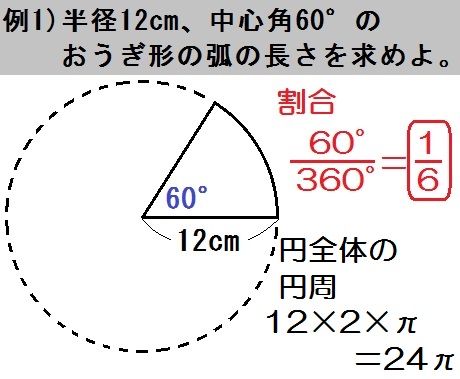
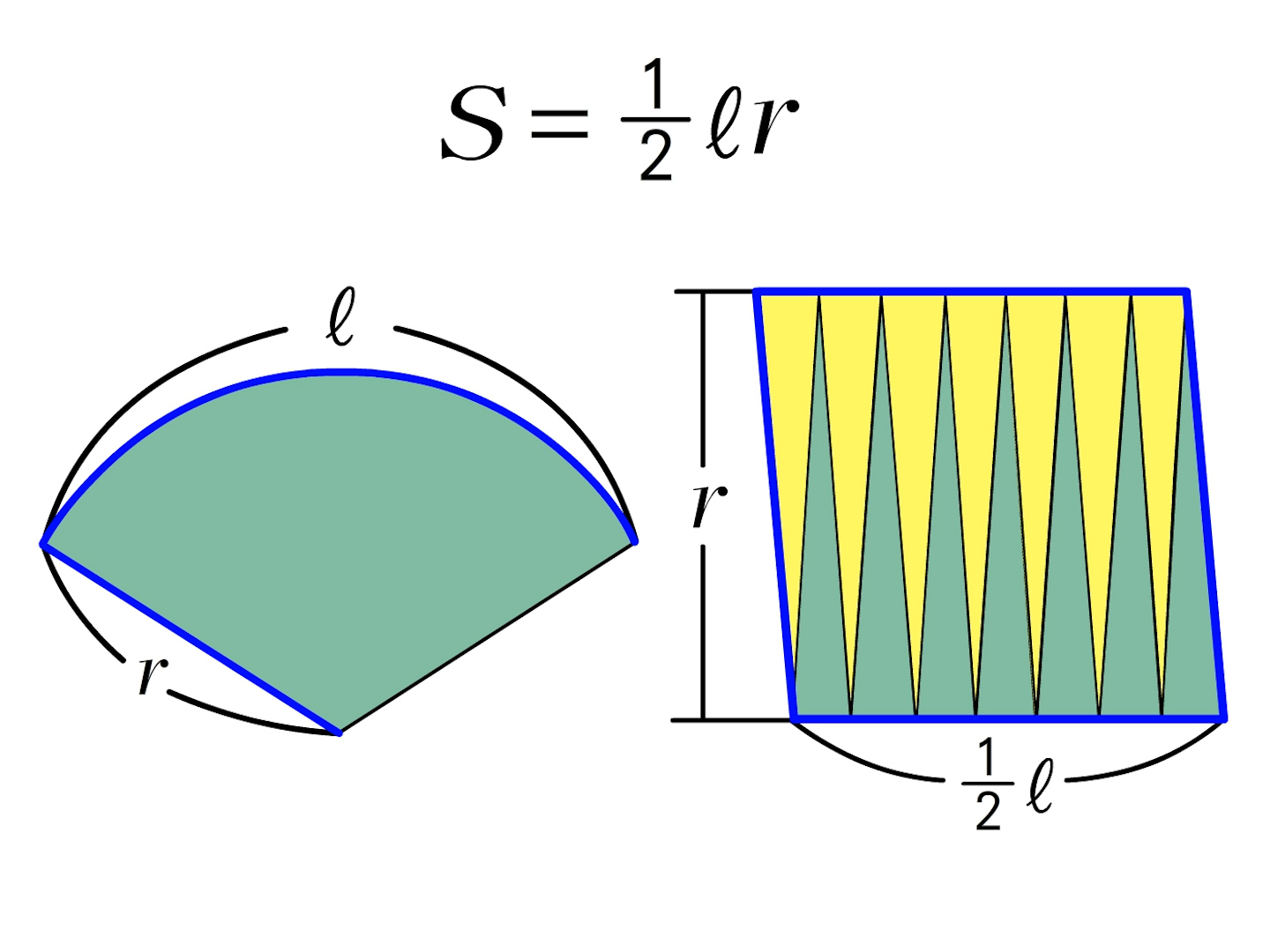
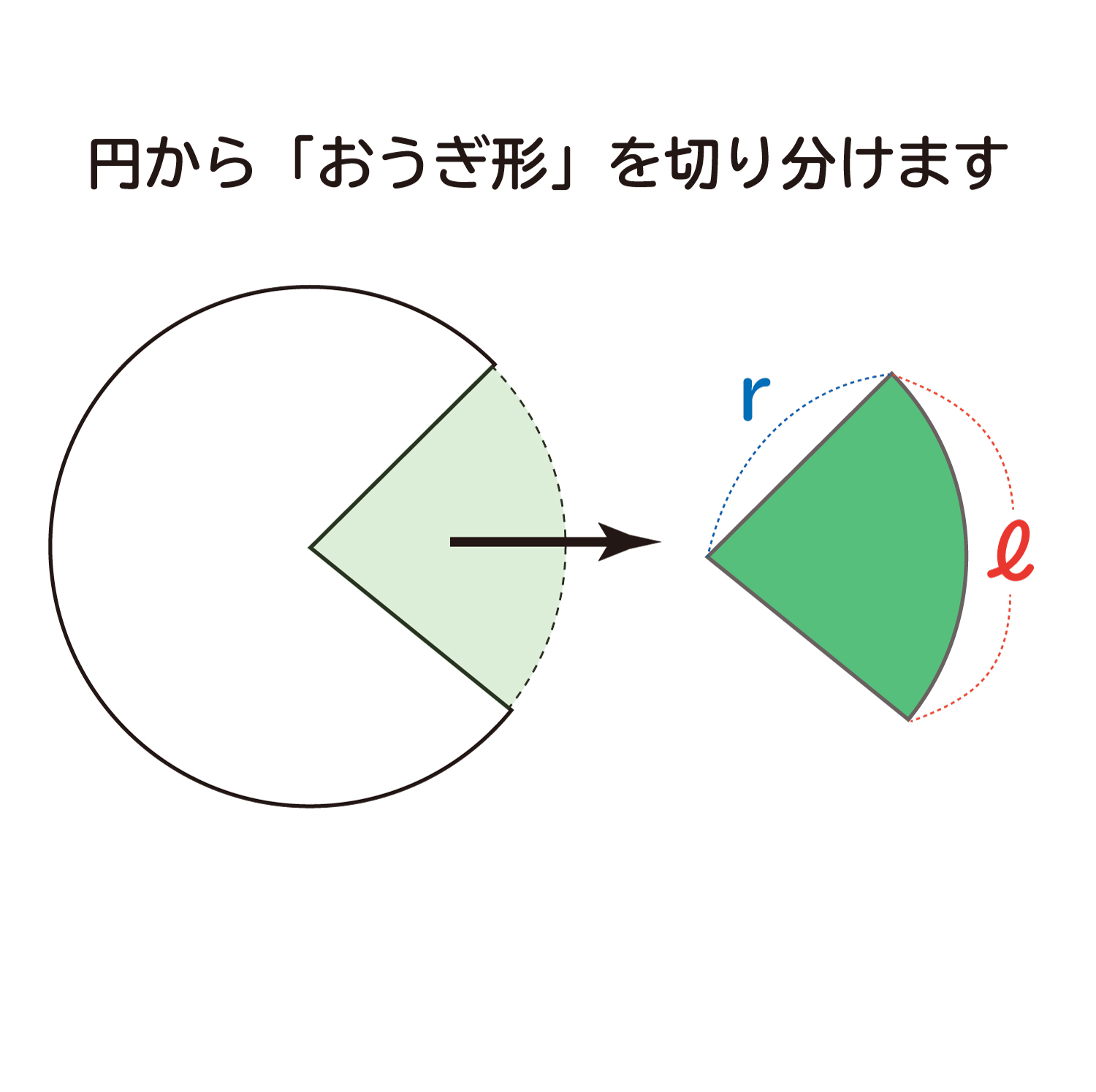
 ・πの意味や円、おうぎ形の周の長さと面積の公式の意味を理解する。 段階 学習活動数学的活動を通した指導のポイント（ は数学的活動をともなう学習活動） つかむ 本時の学習内容「おうぎ形の弧の長さと面積が求められるようになろう」を知る。 教科書147ページの「ひろげよう」 おうぎ形の面積を求める二つの公式のうち、 1 半径×半径×314（円周率）×中心角/360 は 円の面積を求める公式に「×中心角/360」という「おうぎ」おうぎ形の面積を考えてみます。 弧の長さが $l$，半径が $r$ のおうぎ形を細かく切ると平行四辺形のようになります。 おうぎ形の面積は，底辺が $\frac{1}{2}l$，高さ $r$ の平行四辺形の面積と同じに

おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

扇形の面積の公式

扇形の面積の公式-採点する やり直す 解説 3 半径 10 ，中心角が90°の扇形の面積 円の面積の4分の1だから，10 2π ÷4=25 π π 採点する やり直す 解説 4 下の図の灰色で示した図形の面積 扇形の面積は円の4分の1で25 π ，これから三角形の面積 10×10÷2=50 を引く おうぎ形の面積を求める公式 面積=円の面積×中心角の割合 半径5cm、中心角36度のおうぎ形の面積は何cm 2 計算方法は加減法または代入法で選択でき、途中式も表示されます。 弧度法 (ラジアン)今までの角度 (0°,180°,360°等)＝度数法 (「°」 図解講師「爽茶」の最高に分かりやすいサイト そうちゃ's 図解英数ゼミナールしかし，円周の長さ，円の面積など長さや

1

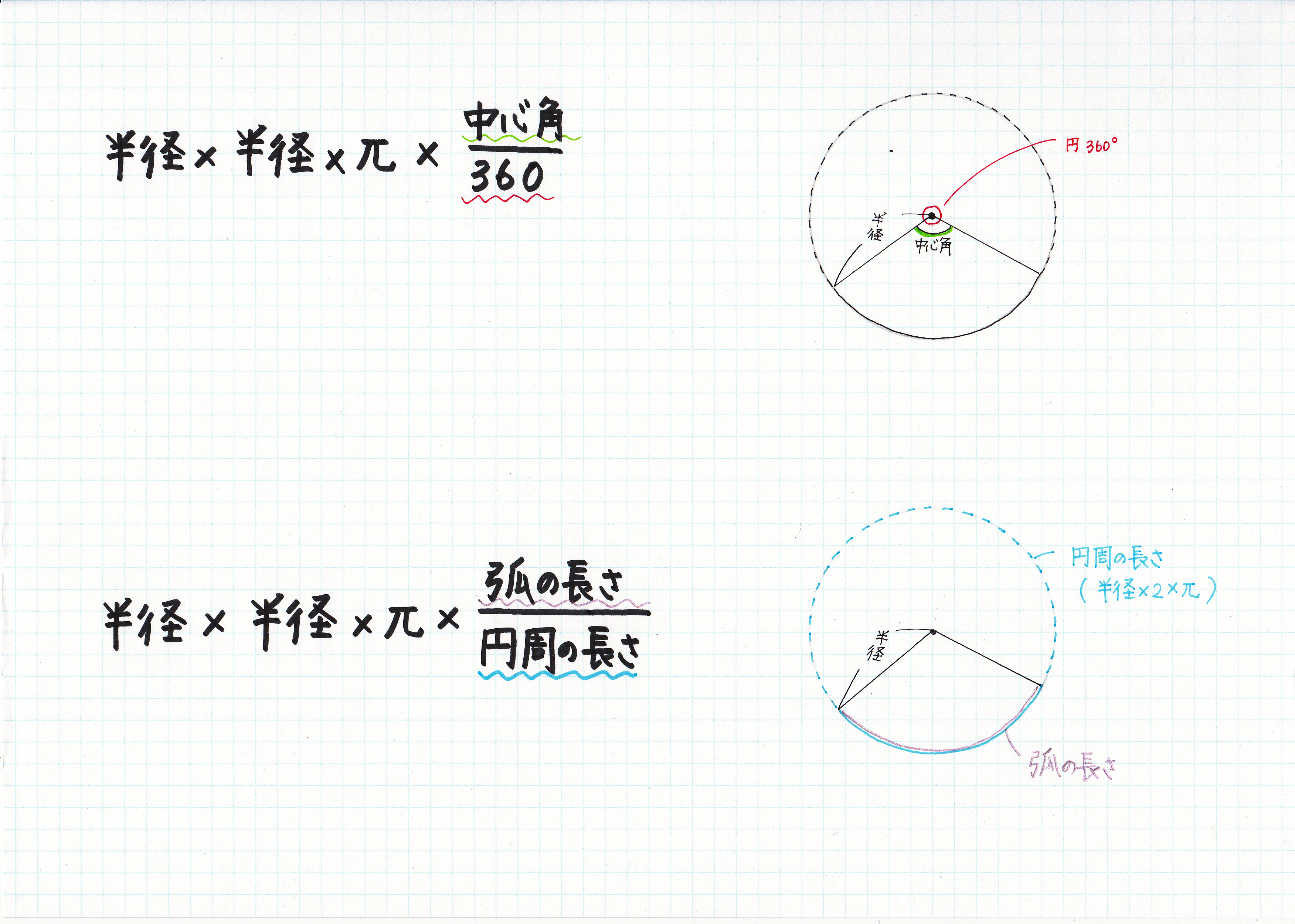
 中心角のわかっている、おうぎ型の 面積 を求める公式 $面積=半径\times半径\times314\times\frac{\displaystyle 中心角}{\displaystyle 360^\circ}$ 面積を2倍 にすると おうぎ形の弧の長さ、面積、中心角の求め方と公式 おうぎ形は円を切りとったものです。 半分だけ切りとれば中心角は180°、さらに半分切りとれば中心角は90°になります。 ケーキを半分に切ったり、三分の一にしたりするときを想像するとわかりやすい 円の面積の公式 方｜小学生に教えるための解説 円周や円の面積について習ったら、次はそれを応用したおうぎ形の弧の長さ・面積について習います。 おうぎ形は『円』と『比』の単元が関係する 4扇形の面積の公式 考え方は弧の長さと同様。 完全な円の面積（\({\pi}r^{2}\)）と比べて

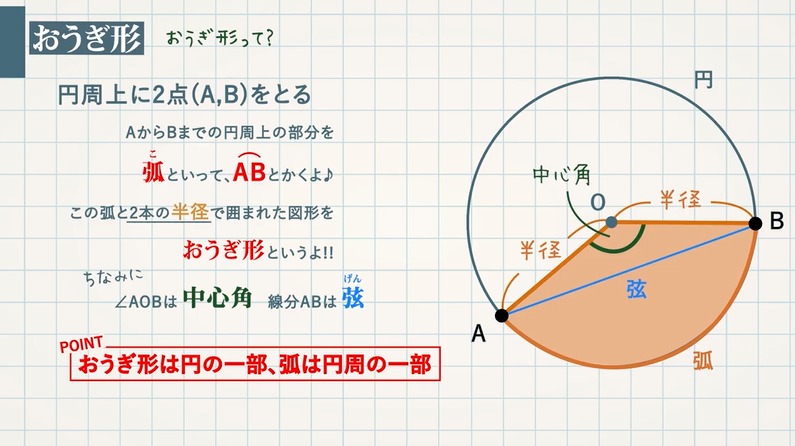
 おうぎ形の面積の求め方1 おうぎ形ABCが存在する時に扇形の面積をSとすると、この面積Sを求める公式は次の (1)式のようになります。 S= 1 2(半径AB)(弧BC) (1) (1) S = 1 2 ( 半 径 A B) ( 弧 B C) この時の比較として三角形DEFも置いておきます。 三角形の面積を求める公式はもちろん 1 2( 1 2 ( 底辺)() ( 高さ)) となります。 1つ目の面積の求め方はおうぎ形を分割していく 中学生公式確認問題①図形編 ①円の面積の公式 （半径をr、円周率をπ） ②円周の長さの公式 （半径をr、円周率をπ） ③おうぎ形の面積の公式 （半径をr、円周率をπ、中心角をx） ④おうぎ形の弧の長さの公式 （半径をr、円周率をπ、中心角をx） おうぎ形の面積の公式と弧の長さの公式は、次の式で表されますね^^ 前半の πr^2（πr2乗） は、 円の面積＝半径×半径×円周率 2πr は、 円周＝直径×円周率 円の公式 だから、分かるね さて どちらの公式にも付いている最後の a/360（360分のa） これが

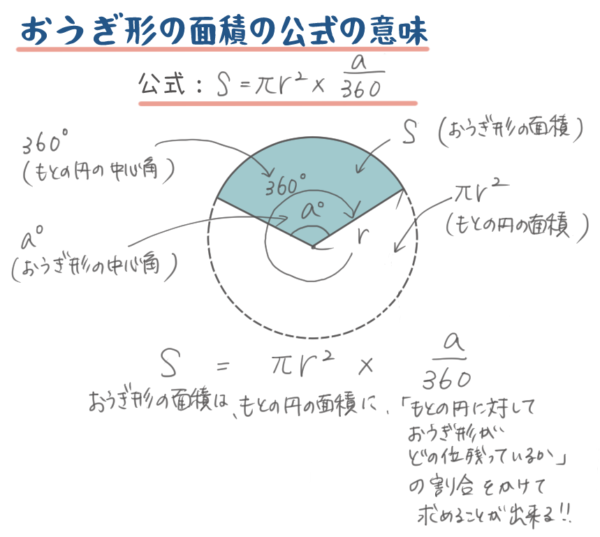
おうぎ形の面積 ＝ 円の面積 × 中心角 360° 中 心 角 360 ° ＝ 半径×半径×314 × 中心角 360° 中 心 角 360 ° 重要なのは、 おうぎ形が元の円と比べた時にどれくらいの割合なのか ということ。 たとえば中心角が 270° 270 ° 、 180° 180 ° 、 90° 90 ° 、 45° 45 ° といったおうぎ形は元の円と比べるとそれぞれ 3 4 3 4 、 1 2 1 2 、 1 4 1 4 、 1 8 1 8 の大きさになっているのは明らか長方形の面積 平面図形 公式 集 確認シート a＝長さ b ＝長さ h＝高さ ℓ＝弧の長さ S ＝面積 V ＝体積 四角柱 四角錐 三角柱 三角錐 円柱 円錐 空間図形 公式集 確認シート a＝長さ b ＝長さ h＝高さ ℓ＝弧の長さ S ＝面積 V ＝体積 Created Date 9/2/08 AM 円すい展開図・側面積の公式 の求め方 一つの式で書く $底円の円周の長さ=r\times2\times314$ $半径Rの円周の長さ=R\times2\times314$ おうぎ形の弧の長さは、底円の円周の長さと同じ長さなので、 $おうぎ形の弧の長さ =r\times2\times314$ おうぎ形と半径Rの円を比べると

おうぎ形の面積の公式 算数の公式

数学質問 おうぎ形の面積の公式について Youtube

 おうぎ形の面積は、 「母線の長さ × 弧の長さ ÷ 2」 という公式で求めることが出来るのですが、その生徒は 「確かこう教わった気がする。あれ？こうじゃなかったっけ？わからん。けどなんとなくこの計算でやってた。おうぎ形 をだんだん そのためには、円の面積の公式 の考え方や、これまで学習してきた「円周率・円周・直径・半径・長方形や正方形の面積の求め方」の基礎的な理解が必要です。 そこで、①目で見てわかるように、算数アニメを使ったり②学習の振り返りのリンクをつけたりしてこれがおうぎ形の公式の意味するところです。 おうぎ形の面積 もう1つの方法 おうぎ形の面積には、もう \(1\) つ覚えておいて損のない公式があります。 おうぎ形の半径を \(r\) 、弧の長さを \(l\) とすると、面積 \(S\) は、 \(S=\)\(\displaystyle \frac{1}{2}\)\(lr\)

おうぎ形の弧の長さと面積 が苦手でもコレなら分かる 中学1年数学 平面図系 教科書をわかりやすく通訳するサイト

円錐の側面積 おうぎ形の面積 と三角形の面積の比較 デジタル教科書 電子教科書

半径と中心角から面積を求める式から、上の式を導いてみましょう。 S = πr2 × x 360 = π× r×r× x 360 = (2πr× x 360)× 1 2 × r S = π r 2 × x 360 = π × r × r × x 360 = ( 2 π r × x 360) × 1 2 × r ここで、弧の長さ l は l = 2πr× x 360 l = 2 π r × x 360 であるから S = l× 1 2 ×r = 1 2lr S = l × 1 2 × r = 1 2 l r となるのです。 続いては、扇形の面積を求める計算問題を解いてみましょう！ おうぎ形で比例式を使うときは、調べたいおうぎ形と半径が同じ円を考えましょう。 つまり、 この2つで考えるということですね。 作る比例式は、以下になります。 おうぎ形の弧の長さ 円の円周＝おうぎ形の中心角：360 おうぎ形の面積 円の面積おうぎ形の面積の公式 \ おうぎ形の面積 = 円の面積 \times \frac{中心角}{360°} \ 円周の公式 \ 円周 = 直径 \times 円周率 \ 円の面積の公式 円の面積 \(=\) 半径 \(\times\) 半径 \(\times\) 円周率 よく読まれている記事 平行四辺形の面積の公式;

おうぎ形の問題 ちょっと応用編 切り取って求める 苦手な数学を簡単に

円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり

 おうぎ形の面積 $$\pi r^2 \times \frac{a}{360}$$ 円の公式を覚えていれば おうぎ形の公式は\(\times \frac{a}{360}\)をくっつけるだけで作ることができますね！弓形の面積＝おうぎ形−直角二等辺三角形 2 赤いおうぎ形−斜線の三角形 1 ＝456(㎠) 3 斜線の弓形を求めて2倍する 1 ＝114(㎠)弓形1個分(☆) 4 半円−直角二等辺三角形 ＝18×π−36 ＝5652−36 ＝52(㎠) 正方形はひし形の公式を使います。 ＝26−18 「 おうぎ形の面積の求め方 」はつぎの公式であらわされるんだ。 半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α / 360

おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ

おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

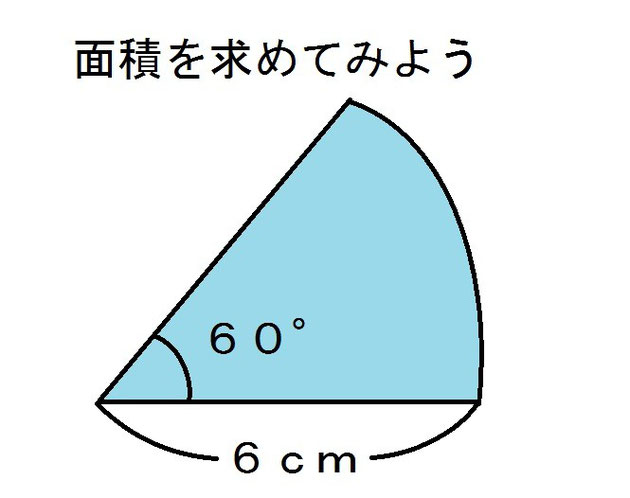
 つぎに面積。 おうぎ形って円の一部だから、おうぎ形の面積＝円の面積の一部です。 だから(円の面積)× \(\frac{1}{4}\) をすればいい。 円の面積は $$ 6 \times 6 \times \pi = 36 \pi $$ よって、求めるおうぎ形の面積は $$ 36 \pi \times \frac{1}{4} = 9 \pi $$ 答．\(9 \pi \) ㎠ と出ます。おうぎ形の面積 は 上記の例のように中心角を求めてから公式に当てはめれば良い。 例題動画 半径と弧から面積を求める S= 1 2 lr (2年) 半径rcm, 弧の長さlcmの おうぎ形の面積をScm 2 とすると, S= 1 2 lr が成り立つ。 面積 S cm 2 弧 lcm 半径 rcm 説明 l=2πr× a 360 ① S=πr 2 × a 360 ② ①をaにつおうぎ形の面積の公式と求め方 教科書には扇形の面積や弧の長さを求める公式があります。 半径を\(\,r\,\)，中心角 \(\,a^\circ\,\) として、 扇形の弧の長さ \(\,\ell\,\) と扇形の面積 \(\,S\,\) の公式は、 \(\color{red}{ \displaystyle \ell=2\pi r \times \frac{a}{360}\\ \displaystyle S=\pi r^2 \times \frac{a}{360}}\) となります

平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト

なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル

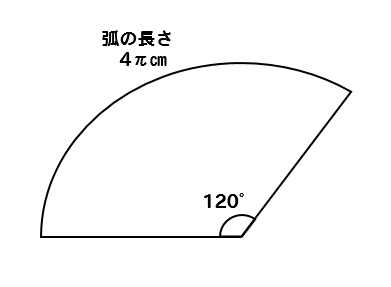
 円錐の側面積の求め方 母線×底面の半径×314 確かにこの公式を覚えておけば側面積を即答できるため、圧倒的に有利なのですが、それは覚えていられる間の話。 もし 忘れたり混乱したりすると、求められなくなってしまう のです。 そこで押さえておきたいのが、 展開図のおうぎ形の弧の長さと底面の円周の長さが等しい ということ。 「そんなの知っ 面積がπ㎝²、中心角が40°であるおうぎ形の半径を求めなさい。 今度は面積が与えられているので おうぎ形の面積の公式に当てはめていきましょう。 すると、このような方程式ができあがります。 これを解いていきましょう！ 両辺をπで割って消し 同じように、おうぎ形の面積を求めると、3π㎠になるよ。 この作業をいっぺんに表したのが教科書の公式 なんだよ。 弧の長さの公式：\(l＝2πr×\frac{a}{360}\)

扇形の弧の長さ 扇形の面積 弧度法 一夜漬け高校数学274 三角関数 Youtube

おうぎ形まとめ 弧と面積の求め方 教遊者

本時の目標 おうぎ形の面積の公式が、円全体との比較から導かれることがわかる。 展開 1．円の面積の求め方の公式を確認する。 2．本時の学習課題を把握する。 円の面積をもとに，おうぎ形の面積を求めよう 3．おうぎ形の面積は円の面積の何分の何になるか考える。 （問）円を半分に折っ 円の面積のまとめ ・円の面積＝半径×半径×314 ・おうぎ形の 面積＝半径×半径×314× 中 心 角 中 心 角 360 ° 弧の長さ＝円周× 中 心 角 中 心 角 360 ° かずのかず 以上、「算数嫌いな人が、 算数を楽しく好きになって欲しい」 かずのかずでした もしおうぎ形ではなく円であれば、面積は πr2 π r 2 なので、比で考えると S πr2 = θ 2π S π r 2 = θ 2 π なので、これを S S について解くと S = 1 2r2θ S = 1 2 r 2 θ となります。 もちろんこれでもいいのですが、弧の長さの式を使ってさらに変形することもでき

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

扇形の中心角の求め方を教えてください 中心角の求め方は２通りのパタ Yahoo 知恵袋

 おうぎ形の公式 おうぎ形の面積は、半径をr、面積をS、円周率をπ、中心角をαとすると、 S = πr² × α おうぎ形の公式おうぎ形の面積は、半径をr、面積をS、円周率をπ、中心角をαとすると、S = πr² × α / 360となります。

1

扇形の面積の求め方 公式と計算例

簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

高校入試対策数学 円錐に関する対策問題 Pikuu

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

おうぎ形の中心角の求め方 Youtube

Studydoctorおうぎ形の公式と忘れない考え方 中学１年数学 Studydoctor

公式を図解 すい体の体積 円すいの表面積の求め方

おうぎ形の面積 弧度法との関連から眺める 身勝手な主張

1

高校数学 一般角と弧度法 扇形の弧長l R8と面積s 1 2r 8 受験の月

扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ

扇形の弧の長さの求め方 公式と計算例

中学数学 円とおうぎ形 中学数学の無料オンライン学習サイトchu Su

円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり

Mathematics 平面図形 おうぎ形 働きアリ

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

おうぎ形 半径の求め方は 問題を使って徹底解説 数スタ

中1数学のおうぎ形の公式が覚えられません そろそろテストなのでやばいんです 今はとに Clear

扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ

中学数学 平面図形 のコツ 円とおうぎ形

円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり

おうぎ形の面積 弧の長さ 数学ノート

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

おう ぎ 形 の 面積 求め 方

おうぎ形の面積の求め方 次世代型個別指導塾アチーブメント Achievement

算数 本当に 分かる という事 身近なおうぎ形 エース学院

1年 おうぎ形の面積 数学イメージ動画集 大日本図書

半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear

円とおうぎ形 応用 無料で使える中学学習プリント

なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル

扇 おうぎ 形の面積を求める公式と弧の長さの求め方

標準 おうぎ形と正方形の面積 なかけんの数学ノート

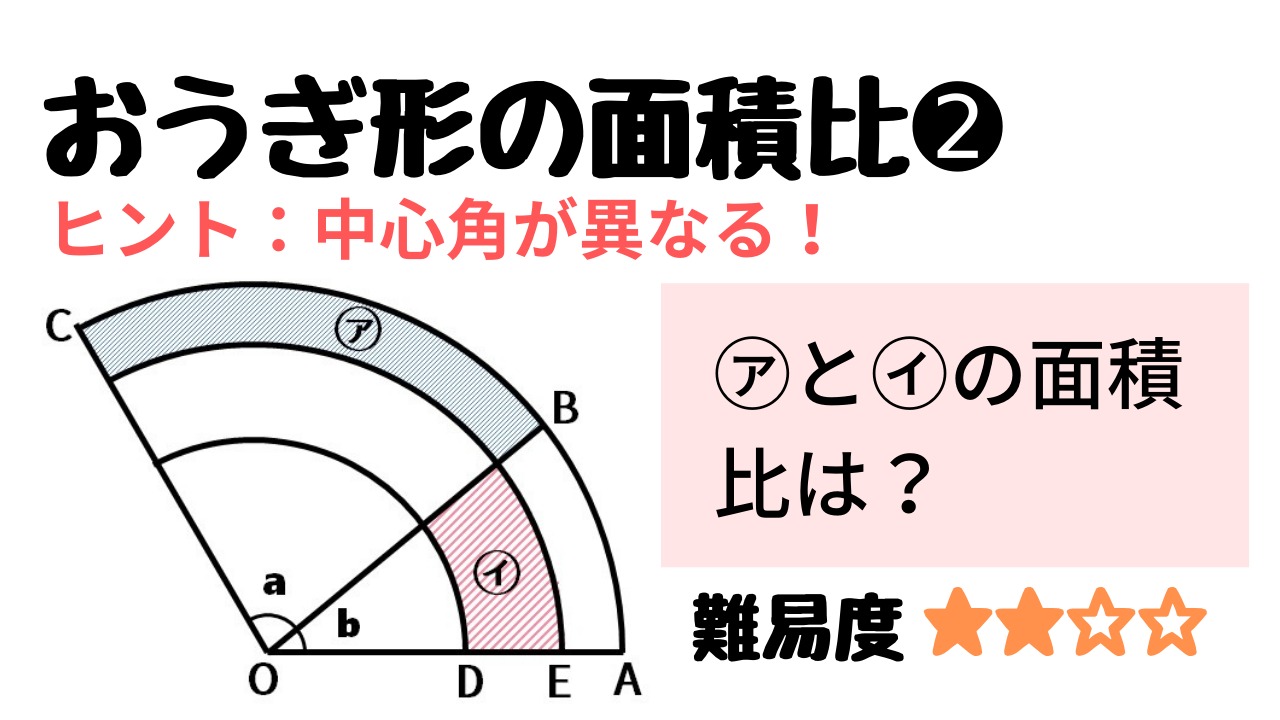
中学受験算数 中心角が異なるおうぎ形の面積比の問題 Stupedia

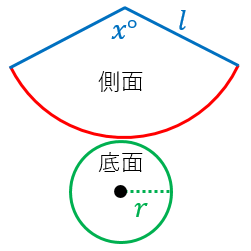
円錐の側面積 底面積 表面積の求め方 具体例で学ぶ数学

計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

扇形の弧の長さと面積 小学 中学数学での平面図形の求め方 リョースケ大学

円 扇形 の面積 周や弧の長さの公式 数学fun

おうぎ形の面積と弧の長さの公式 全国 中学数学ができるようになるブログ

裏技 おうぎ形の面積を一瞬で求める 弧の長さを利用した裏技公式 中学数学 平面図形 ２ Youtube

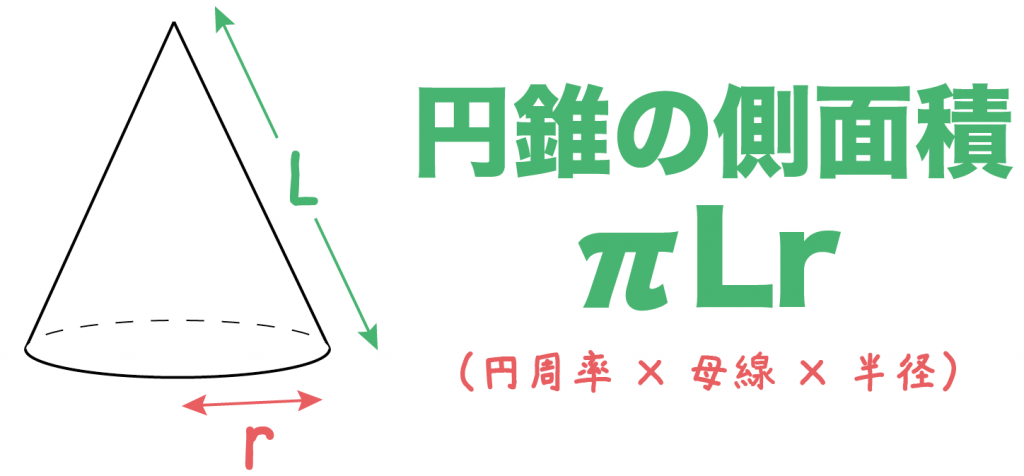
簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

ラブリー扇形 弧の長さ 公式 最高のカラーリングのアイデア

円錐の表面積 あんず学習塾のメモ 図表置き場

扇の弧の長さと面積の求め方 公式 中学数学 By Okボーイ マナペディア

これを教えてください なぜ S 2分の1lr の式が成り立つのですか Clear

扇形の面積 弧の長さ まわりの長さの求め方 公式 小学生 中学生の勉強

正方形と扇形の面積をつかった問題がわかる3ステップ Qikeru 学びを楽しくわかりやすく

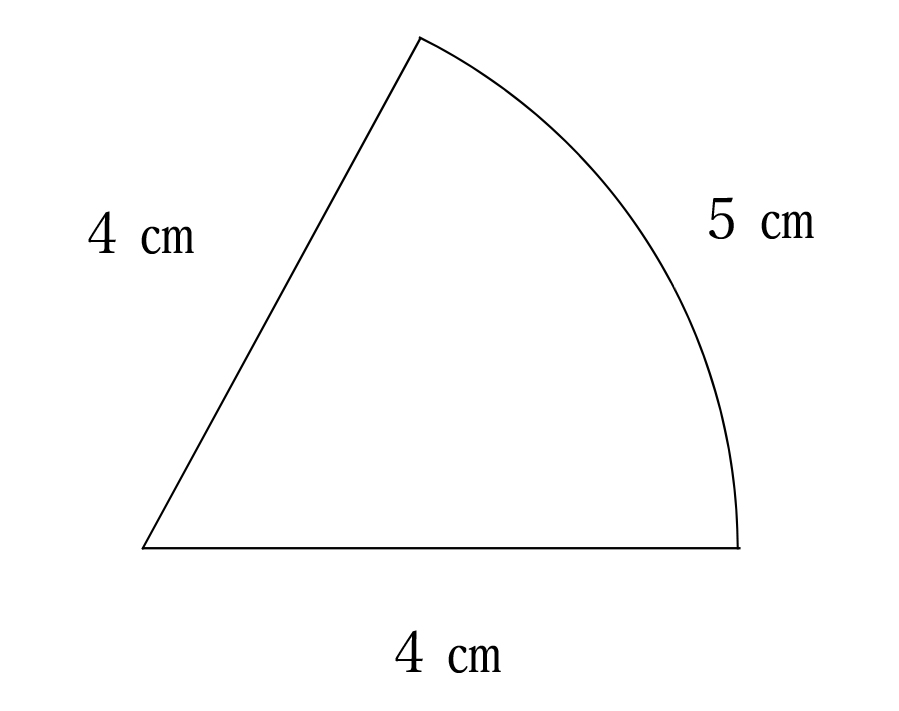
おうぎ形の弧の さと 積の求め方 中学受験プロ講師ブログ

扇形面積の求め方 扇形の面積公式が一目でわかる 丁寧な証明付き 高校 Qkaxtw

3

扇形の弧の長さの公式 簡単な問題で求め方をマスターしよう 中学や高校の数学の計算問題

側面のおうぎ形の弧の面積の公式 側面積lrpのもとになっているpl 2 X 数学 教えて Goo

扇形の面積の出し方と特殊な場合の公式 たぬぬ塾 中学校の先生たち

おうぎ形の弧の長さと面積の求め方 小学生に教えるための解説 数学fun

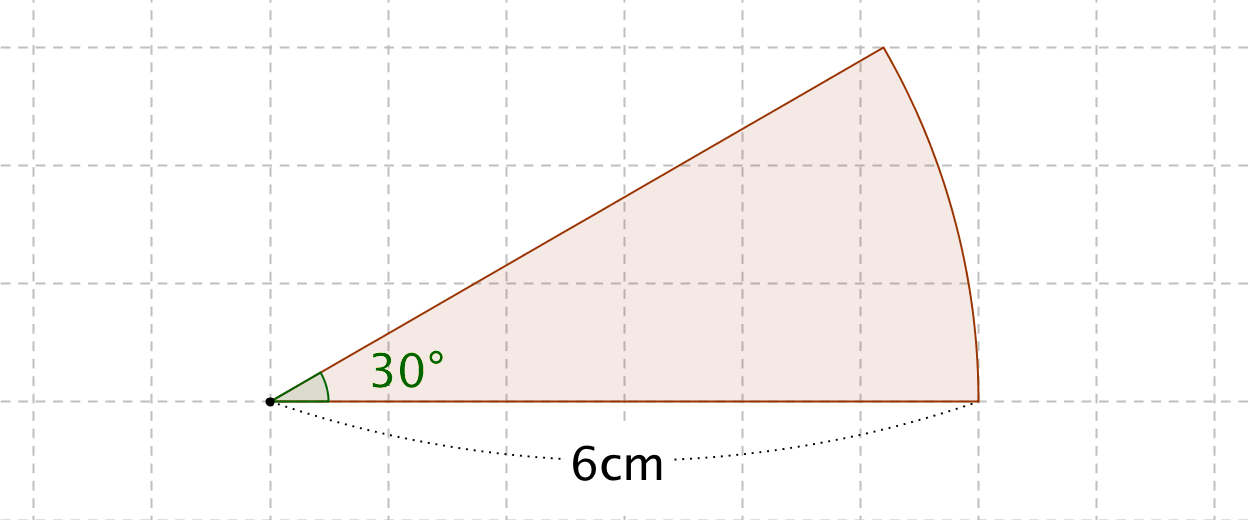
おうぎ形の面積の公式 算数の公式

扇形の面積の求め方 公式と計算例

扇形面積公式弧長14 Zilhc

おうぎ形面積の超簡単な求め方 合同会社エスキージャパン

扇形の面積の求め方 小学生でも公式を簡単に使える問題です 中学や高校の数学の計算問題

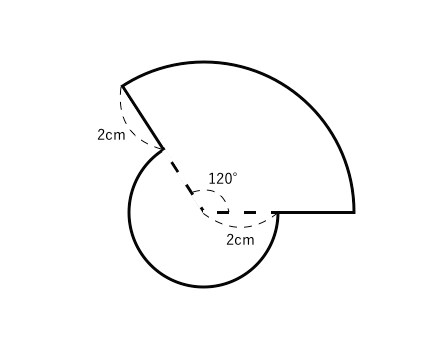
おうぎ形の問題 ちょっと応用編 苦手な数学を簡単に

至急です 扇形の面積の公式を使って色がついている部分の面積を求めなさいという問題です Clear

小学校6年生の算数 数学fun 数学 小学校 算数 算数

円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

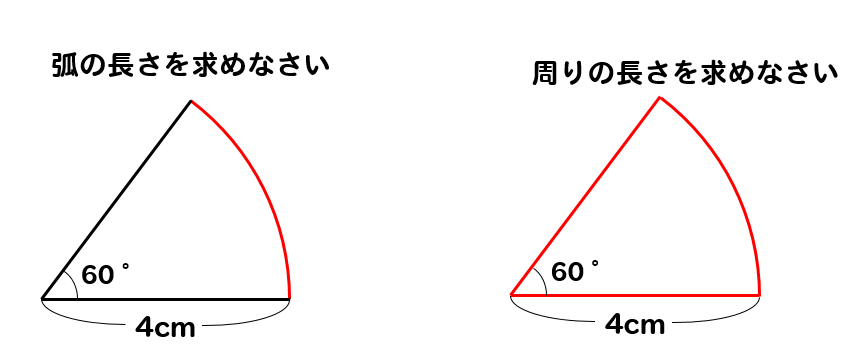
おうぎ形 注意 周りの長さを求める公式を解説 数スタ

1

扇形面積公式弧長 3分で分かる 扇形 おうぎ形 の面積と弧の長さの Mtlpe

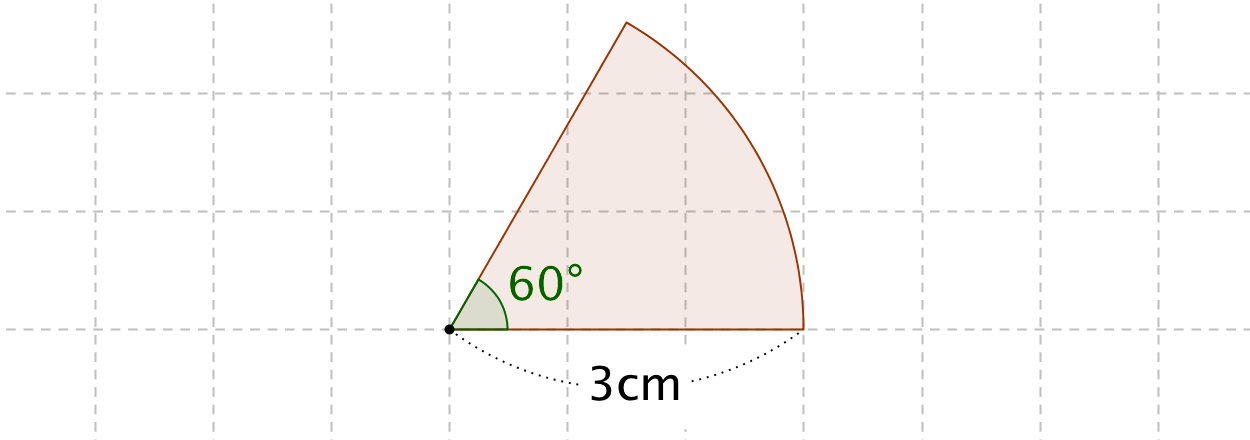
おうぎ形の面積の公式 算数の公式

おうぎ形 色のついた面積の求め方 数学の記録

中1数学 円とおうぎ形 では 円の性質とおうぎ形の面積の求め方が項目理解の重要ポイント 桜華塾 お役立ちブログ 楽天ブログ

円とおうぎ形の周りの長さ 面積の求め方 無料プリントあり

なぜ おうぎ形の面積は1 2 弧の長さ 半径 なのか を説明します おかわりドリル

おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方

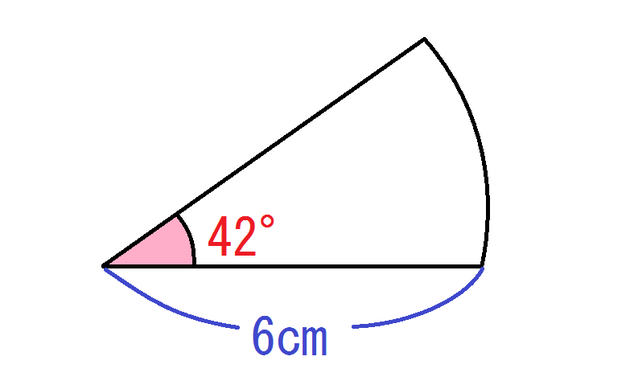
算数 本当に 分かる という事 おうぎ形の面積その２ エース学院

中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube

中学１年生 数学 円とおうぎ形 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生

中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく

おうぎ形の弧長 面積 中心角 半径 具体例で学ぶ数学

弧の長さを使った扇 おうぎ 型の面積の公式を知っていますか

標準 おうぎ形の弧の長さや面積 なかけんの数学ノート

高校入試数学 おうぎ形についての公式まとめとその練習問題

3分で分かる 扇形 おうぎ形 の面積と弧の長さの求め方 公式をわかりやすく 合格サプリ

面積の求め方 算数の教え上手 学びの場 Com

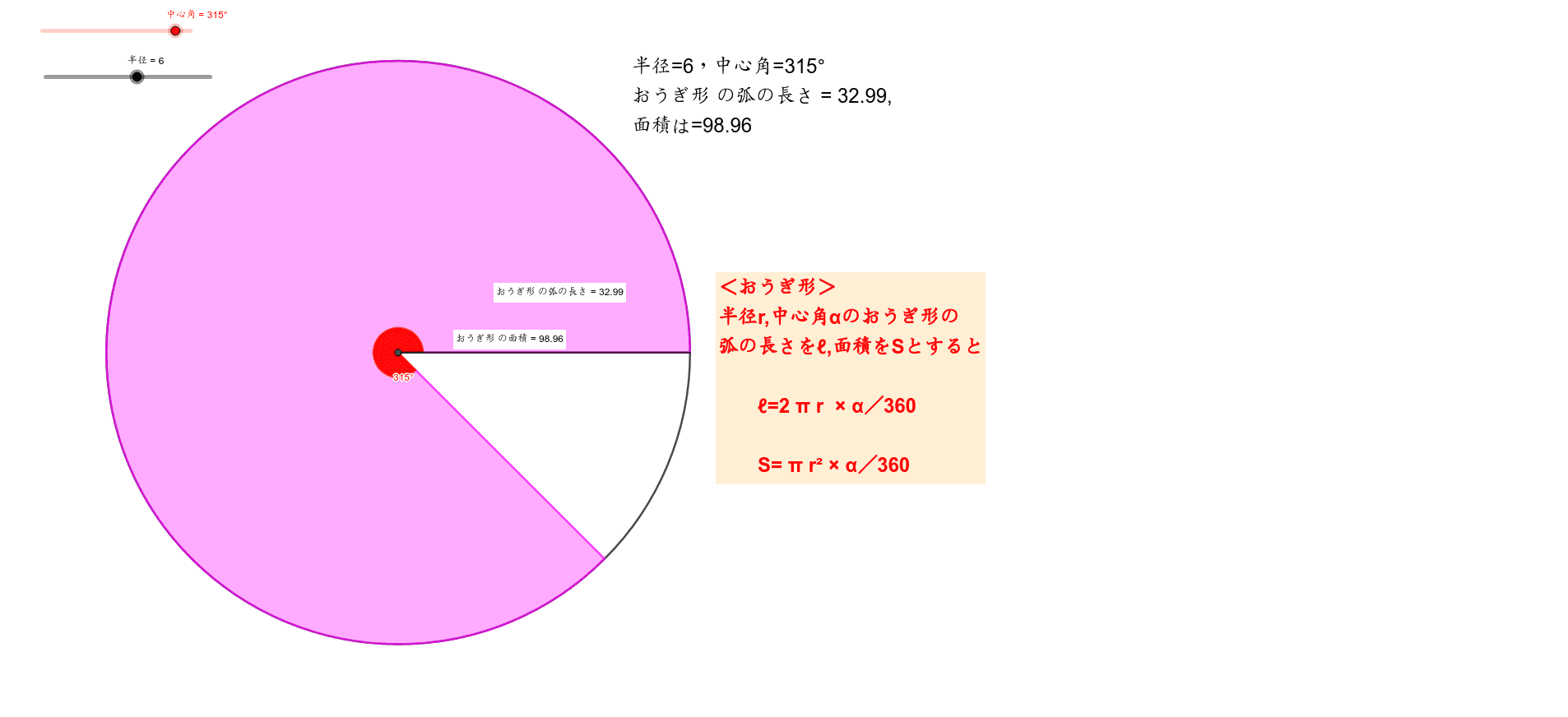
中1 おうぎ形の弧の長さや面積について考えよう Geogebra

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

中1数学 おうぎ形の面積 弧の長さ 中心角の求め方がサクッとわかる 映像授業のtry It トライイット

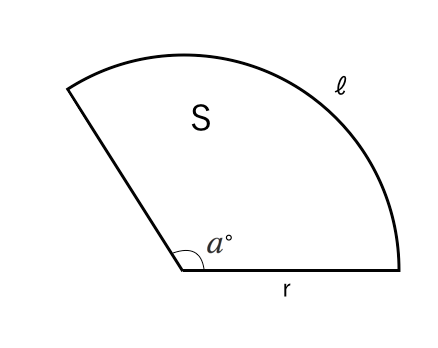
おうぎ形の問題 パターンを知ろう 苦手な数学を簡単に

扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典

Incoming Term: おうぎ形の面積の公式, おうぎ形の面積の公式 簡単, おうぎ形の面積の公式 中学, 扇形の面積の公式, 数学 おうぎ形の面積の公式,